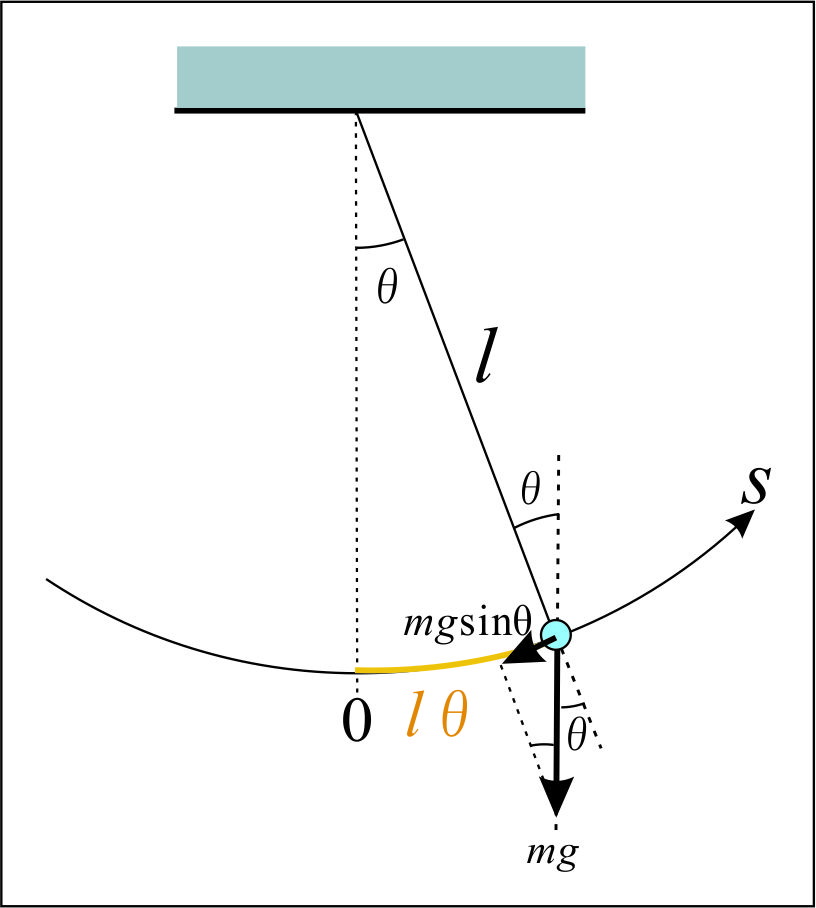
質量$m$の小球$A$が、質量を無視できる長さ $\ell$ の伸びない糸でつり下げられている。 小球Aがつりあう位置をOとする。 小球Aを少し横へ引いて手を放すと振動をはじめる。 糸の長さに比べて振幅が十分小さいものとし、重力加速度を$g$とする。 小球AのOから$x$だけ変位した点を通っているとき、糸が鉛直方向となす角を$\theta$とすると、
小球Aの位置sは、半径$\ell$、中心角$\theta$のおうぎ形の弧の長さに等しいから、 $$s= \ell\theta　\cdots(ア)$$ と表される。
(ア)の両辺を時間$t$で微分すると、 $$\frac{ds}{dt}=\ell\cdot\frac{d\theta}{dt}$$ $$\therefore　\frac{d^2s}{dt^2}=\ell\cdot\frac{d^2\theta}{dt^2}　\cdots(イ)$$ 運動方程式をたてると、 $$m\frac{d^2s}{dt^2}=-mg\sin\theta$$ (イ)より、 $$m\cdot\ell\cdot\frac{d^2\theta}{dt^2}=-mg\sin\theta$$ $$\therefore　\frac{d^2\theta}{dt^2}=-\frac{g}{\ell}\cdot\sin\theta　\cdots(ウ)$$ よって、 $$\omega =\sqrt{\frac{g}{\ell}}　\cdots(エ)$$ とおくと、 $$\therefore　\frac{d^2\theta}{dt^2}=- \omega^2\cdot\sin\theta　\cdots(オ)$$ となる。
いま、$\theta$が非常に小さい、つまり、$|~\theta~| \ll 1$ として考えると、 $$\sin\theta \approx \theta$$ となるので、(オ)に適用すると、 $$\therefore　\frac{d^2\theta}{dt^2}=- \omega^2\cdot\theta　\cdots(カ)$$ となる。
これは、 $$『~角振動数\omega の単振動になる~』$$ ことを表している。
このとき、周期Tは $$周期~T=\frac{2\pi}{\omega}=2\pi\sqrt{\frac{\ell}{g}}　\cdots(キ)$$ である。
(カ)を満たす一般解は、 $$\theta = A\sin\left(\omega t + \delta\right)　\cdots(ク)$$ で与えられ、 $$初期条件~t=0のとき、\theta=\theta_0、\dfrac{d\theta}{dt}=0$$ であるので、(ク)より、 $$\frac{d\theta}{dt}=A\omega\cos(\omega t+ \delta)$$ である。
$t=0のとき\dfrac{d\theta}{dt}=0$であることにより、 $$\delta = \dfrac{\pi}{2}$$ このとき、(ク)は $$\theta = A\sin\left(\omega t + \dfrac{\pi}{2}\right)　\cdots(ケ)$$ となるが、$t=0のとき\theta=\theta_0$であるから、(ケ)に代入して、 $$A=\theta_0$$ よって、この単振動は $$\therefore　\theta(t) = \theta_0\cdot\sin\left(\sqrt{\frac{\ell}{g}}\cdot t + \dfrac{\pi}{2}\right)　\cdots(コ)$$ なる時間の関数$\theta(t)$で与えられる。

ここで、エネルギーについて考えよう。

(イ)、(ウ)より、 $$\frac{d^2s}{dt^2}= -g\sin\theta $$ $$\frac{ds}{dt}\cdot \frac{d}{dt}= -g\sin\theta　\cdots(サ) $$ ここで、(ア)より、 $$ds =\ell\cdot d\theta$$ なので、(サ)は $$\frac{ds}{dt}\cdot \frac{d}{dt}\cdot ds= -g\sin\theta\cdot\ell\cdot d\theta　\cdots(サ) $$ $$\frac{ds}{dt}\cdot \frac{d}{dt}\left(\frac{ds}{dt}\right)\cdot dt = -g\ell\cdot\sin\theta\cdot d\theta$$ ここで、$\dfrac{ds}{dt}= v$ とおくと、 $$\int v\cdot \frac{d}{dt}(v)\cdot dt = -g\ell\int\sin\theta\cdot d\theta$$ $$\frac{1}{2}v^2 = gl\cos\theta + C $$ $$\therefore \frac{1}{2}mv^2 = mgl\cos\theta + C_1 　\cdots(シ)$$ 初期条件 t=0の時、$\theta=\theta_0で、v=0$より、 $$\therefore C_1 =- mgl\cos\theta_0$$ よって、(シ)に代入して、 $$\therefore \frac{1}{2}mv^2 = mgl\cos\theta - mgl\cos\theta_0$$ $$\therefore \frac{1}{2}mv^2 + mgl(\cos\theta_0 - \cos\theta) = 一定　\cdots(ス)$$ となる。
ここで、位置エネルギーは、どこを基準として考えるかによって値は変化するので、 小球Aの最下点、つまり $\theta_0=0$ を基準にとれば、$\cos\theta_0=1$ となるので、 $$\therefore \frac{1}{2}mv^2 + mgl(1 - \cos\theta)~ =~ 一定　\cdots(セ)$$ という、よく知られた「力学的エネルギー保存の法則」の結果になる。