今回は、「単振動の典型問題」についての話題その2です。。。
では、さっそく、考えてみましょう。
問題
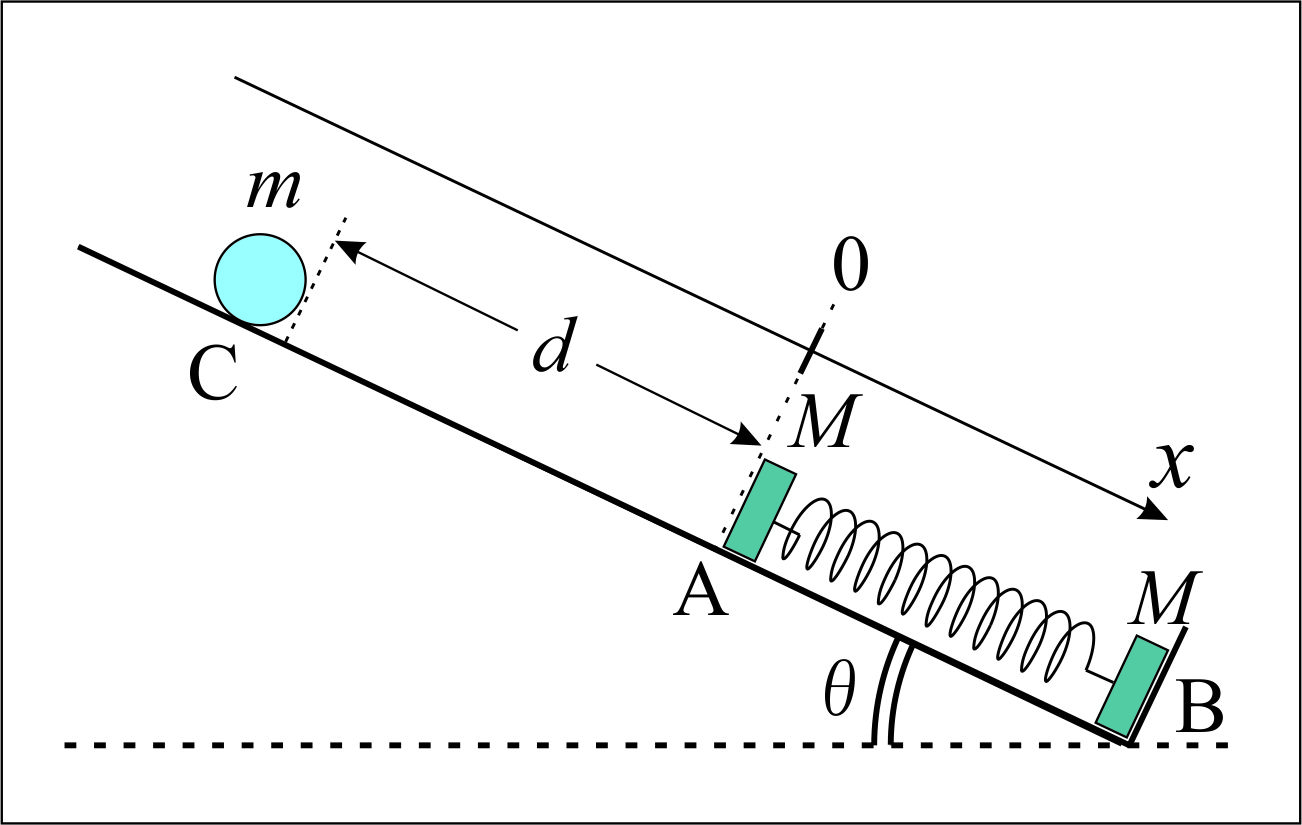
図のように、斜角 $\theta$ の滑らかな斜面上に、 質量 $M$ の物体Aと物体Bが軽いばねの両端に結ばれて自然長から $a$ だけ縮んだ位置 $0$ で静止している。 質量$m$ ($m < M$) の小球Cを物体Aから $d$ だけ離して静かに置いたところ、 斜面上をすべり降り、Aと1回目の弾性衝突した。 その後、小球Cは斜面上を上昇するが、 初めてばねが最も伸び切る前に、小球CのAとの2回目の衝突は起こらないものとする。
また、斜面に平行に $x$ 軸をとり、 はじめの $A$ の位置を原点($x=0$)とし、重力加速度を $g$ とする。
このとき、以下の各問いに答えなさい。

図のように、斜角 $\theta$ の滑らかな斜面上に、 質量 $M$ の物体Aと物体Bが軽いばねの両端に結ばれて自然長から $a$ だけ縮んだ位置 $0$ で静止している。 質量$m$ ($m < M$) の小球Cを物体Aから $d$ だけ離して静かに置いたところ、 斜面上をすべり降り、Aと1回目の弾性衝突した。 その後、小球Cは斜面上を上昇するが、 初めてばねが最も伸び切る前に、小球CのAとの2回目の衝突は起こらないものとする。
また、斜面に平行に $x$ 軸をとり、 はじめの $A$ の位置を原点($x=0$)とし、重力加速度を $g$ とする。
このとき、以下の各問いに答えなさい。
- ばね定数を求めよ。
- 1回目の弾性衝突直後の物体Aと小球Cのそれぞれの速度$v_A'$、$v_C'$ を求めよ。
- 1回目の衝突後にばねが最も縮んだときの、その縮みの長さ $\ell_0$ を求めよ。
- 1回目の衝突後、物体Bが壁から離れないための $d$ の条件を求めよ。
-
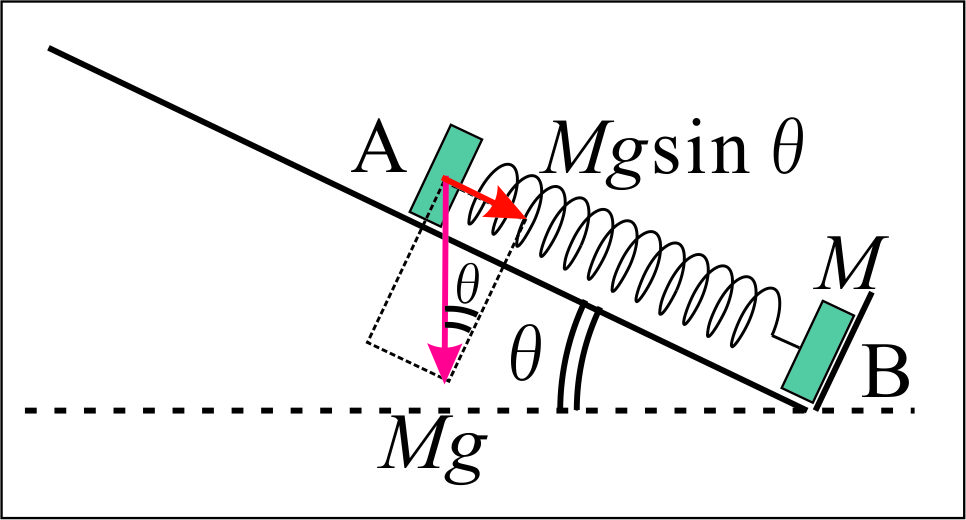
ばね定数を $k$ とおいて、運動方程式を立てると、図より、 $$M\alpha = Mg\sin\theta - ka \cdots(ア)$$ つりあって静止しているとき、加速度 $\alpha$ は 0 なので、 $$Mg\sin\theta - ka = 0$$ $$\therefore k = \frac{Mg\sin\theta}{a} \cdots(イ)$$ - 物体Aと小球Cの衝突直前の小球Cの速度 $v_C$ は
$${v_C}^2-0^2=2\cdot g\sin\theta\cdot d$$
$$\therefore v_C = \sqrt{2dg\sin\theta} \cdots(ウ)$$
また、衝突前後の運動量保存則により、
衝突前のAとCの速度を $v_A$ 、$v_C$ とし、衝突後の A と C の速度を $v_A'$、$v_C'$ とすると、 $$mv_C+Mv_A = mv_C' + Mv_A'~ \cdots(エ)$$ また、弾性衝突より、跳ね返り係数 $e=1$ より、 $$-\frac{v_C'-v_A'}{v_C-v_A}=1$$ $$-\frac{v_C'-v_A'}{v_C-0}=1$$ $$\therefore v_A'=v_C+v_C'~ \cdots(オ)$$ (エ)、(オ)より、 $$\therefore v_C' = -\frac{M-m}{m+M}v_C、v_A' = \frac{2m}{m+M}v_C$$ よって、(ウ)より、 $$\therefore v_C' = -\frac{M-m}{m+M}\sqrt{2dg\sin\theta} \cdots(カ) //$$ $$\therefore v_A' = \frac{2m}{m+M}\sqrt{2dg\sin\theta} \cdots(キ) //$$ - 力学的エネルギー保存の法則により、 $$\frac{1}{2}{Mv_A'}^2 = \frac{1}{2}\cdot M \cdot 0^2 + \frac{1}{2}k{\ell_0}^2$$ $$\ell_0 = \sqrt{\frac{M}{k}}\cdot v_A'$$ $$\ell_0 = \sqrt{\frac{a}{g\sin\theta}}\cdot v_A'$$ $$\ell_0 = \sqrt{\frac{a}{g\sin\theta}}\cdot \frac{2m}{m+M}\sqrt{2dg\sin\theta}$$ $$\therefore \ell_0 = \frac{2m}{m+ M}\sqrt{2ad} \cdots(ク) //$$
- (3)より、1回目の衝突後のばねの振幅が $\ell_0$ になる。
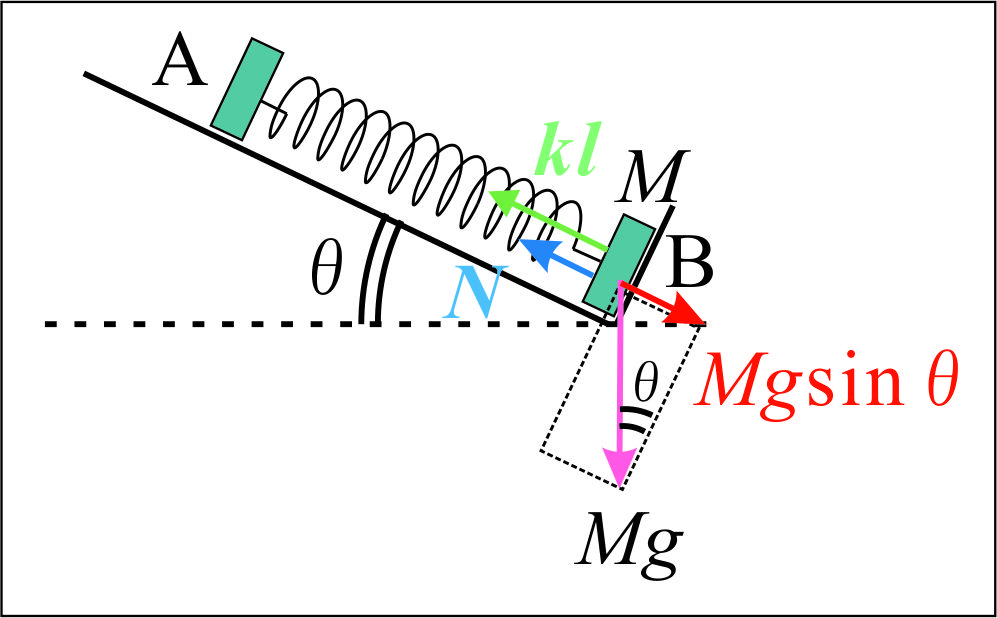
ここで、ばねが最も伸び切ったときの物体Bの垂直抗力 $N$ を考えると、 $$N = Mg\sin\theta~ - ~k\cdot \ell_0 \cdots(ケ)$$ 物体Bが壁から離れない条件は $$N > 0$$ であるので、(ケ)より、 $$Mg\sin\theta~ - ~k\cdot \ell_0 > 0$$ $$\ell_0 < \frac{Mg\sin\theta}{k}$$ (イ)より、 $$\therefore \ell_0 < a$$ (ク)より、 $$\frac{2m}{m+ M}\sqrt{2ad} < a$$ $$\frac{8m^2d}{(m+ M)^2} < a$$ $$\therefore d < \frac{(m+M)^2}{8m^2}\cdot a //$$
いかがでしたか。
理解は出来ましたか?
では、また次回にお会いしましょう。