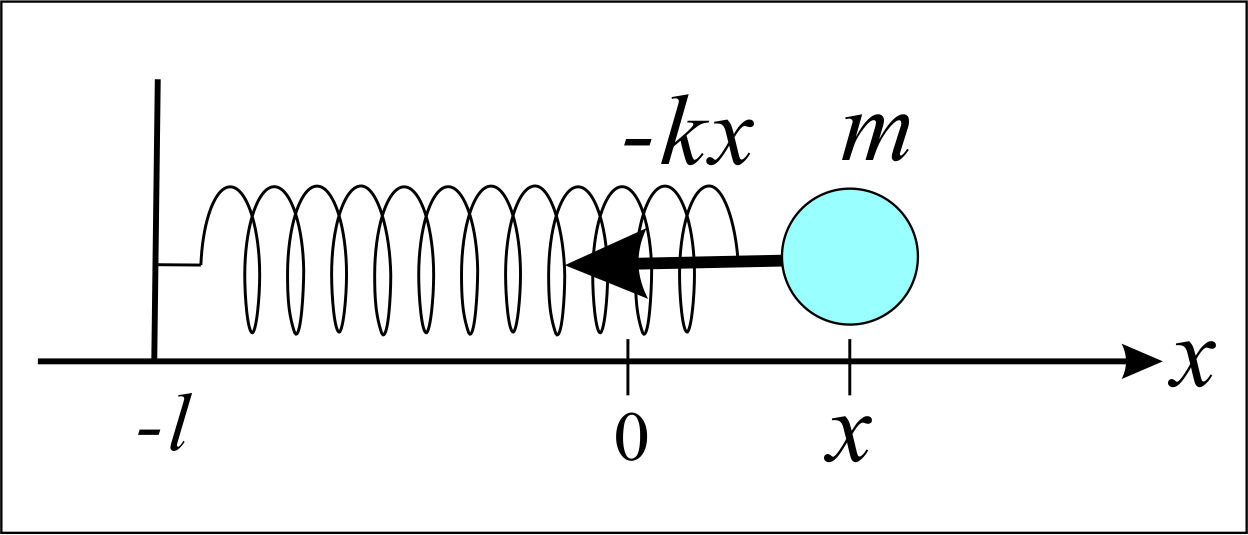
図のように、水平面上で一端を固定されたばねに付けられた質 $m$ の質点Pの運動を考える。 ばねの自然長は $\ell$ である。
フックの法則より、復元力Fは、 $$F=-kx　(k>0)　\cdots(ア)$$ で与えられることが知られている。$k$は、「ばね定数」という。
時刻 $t=0$ の時に質点Pは $x=0$にあり、自然長で静止している状態にあるとするとき、質点Pの運動方程式は $$m\frac{d^2x}{dt^2}=-kx　\cdots(イ)$$ ここで、 $$\omega = \sqrt{\frac{k}{m}}　\cdots(ウ)$$ とおくと、 $$\frac{d^2x}{dt^2} = -\omega^2x　\cdots(エ)$$ となる。
ここで、微分方程式 (エ) の特殊解である $x=\sin \omega t、x=\cos\omega t$ はともに満たす。 この特殊解の1次結合をつくると、それは元の方程式の解であり、すべての解を含む「一般解」であることが 知られている。

$A$ 、$B$ を任意定数とすると、一般解は $$\therefore　x = A\cos \omega t + B\sin \omega t　\cdots(オ)$$ で表される。
ここで、時刻$t=0$のときに自然長から$L$だけ伸ばして、静かに放したとするとき、
$$初期条件 t=0 のときx=L、 \dfrac{dx}{dt}=0$$ なので、$t=0$のとき$x=L$ より、 $$L = A\cos 0 + B\sin 0$$ $$\therefore A = L$$ となり、 $$x = L\cos\omega t + B\sin \omega t$$ これを、時刻 $t$ で微分して、$t=0$ のとき $\dfrac{dx}{dt}=0$ より、 $$\frac{dx}{dt} = -L\omega\sin 0 + B\omega\cos 0 = 0$$ $$\therefore　B=0$$ 以上より、(オ)から、 $$\therefore　x= L\cos\omega t　\cdots(カ)$$ 運動方程式(イ)で与えられる運動方程式において、 $$振動の中心が x=0$$ $$角振動数 \omega =\sqrt{\frac{k}{m}}$$ $$振幅 L$$ の単振動をする。
また、単振動の周期 T は、 $$T=\frac{2\pi}{\omega}=2\pi\sqrt{\frac{m}{k}}$$ で与えられる。

続いて、エネルギーについて考えよう。

運動方程式(イ)において、 $$m\frac{dx}{dt}\cdot\frac{d}{dt} = -kx\cdot\frac{dx}{dt}\cdot\frac{dt}{dx}$$ $$m\frac{dx}{dt}\cdot d\left( \frac{dx}{dt}\right) =-kx\cdot dx$$ ここで、$\dfrac{dx}{dt}=v$ とおくと、 $$mv\cdot dv = kx\cdot dx$$ $$\int mv\cdot dv = \int kx\cdot dx$$ $$\frac{1}{2}mv^2 =-\frac{1}{2}kx^2 + C$$ よって、 $$\frac{1}{2}mv^2 +\frac{1}{2}kx^2 =　一定　\cdots(キ)$$ が成立する。
ここで、 $$運動エネルギー：\frac{1}{2}mv^2$$ $$弾性エネルギー(位置エネルギー)：\frac{1}{2}kx^2$$ と言って、(キ)は、『非保存力が働かない限り』、 $$弾性エネルギーと運動エネルギーの和が保存される$$ ということを意味する。