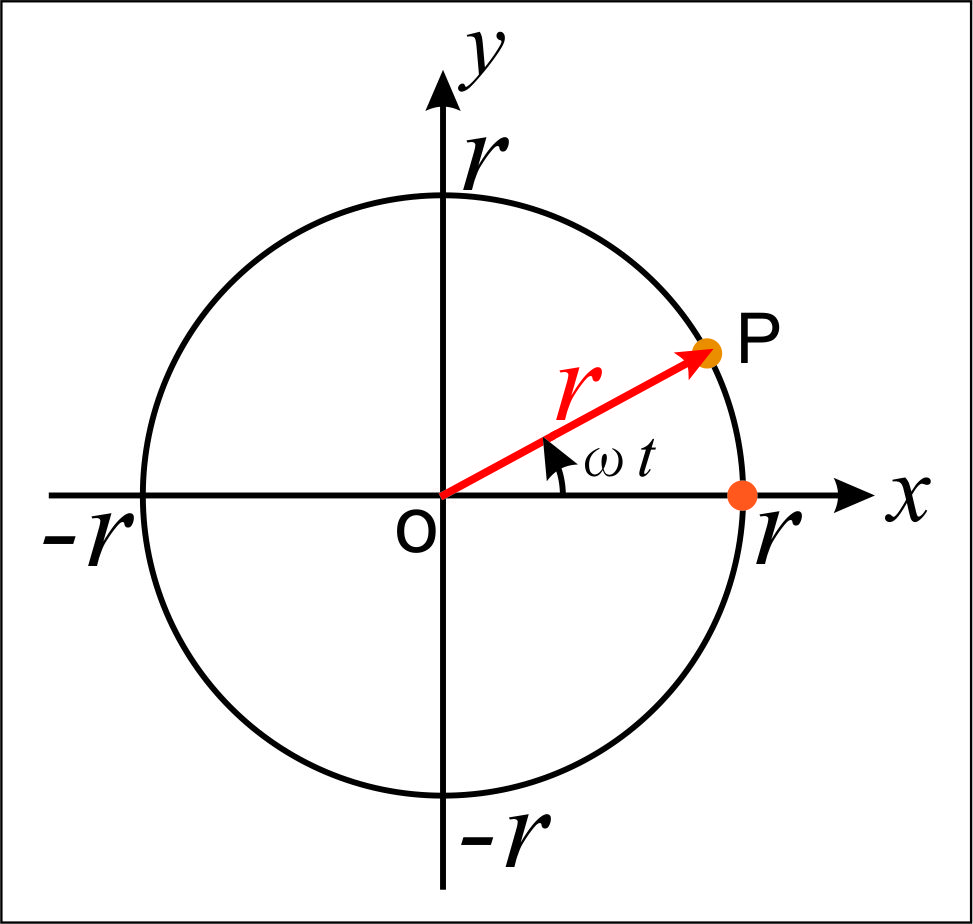
図のように、質量$m$の質点Pが原点Oを中心とする半径 $r$ 、角速度 $\omega$ の等速円運動を している。質点Pは時刻$t=0$のとき、点($r, 0$)を通過し反時計回りに回転するものとする。


ここで、角速度 $\omega$ は、 $$\omega = \frac{\Delta \theta}{\Delta t}　\cdots(ア)$$ で表され、「単位時間あたりの回転角」を表しています。
位置ベクトル $r(t)$ は $$\therefore \overrightarrow{r(t)} = (x(t), y(t))=(r\cos\omega t,r\sin\omega t)　\cdots(イ)$$ と表される。
速度を考えて、 $$\overrightarrow{v(t)}=\frac{d r(t)}{dt}$$ $$= (v_x(t), v_y(t))$$ $$= \left(\frac{d x(t)}{dt}, \frac{d y(t)}{dt} \right)$$ $$= (-r\omega \sin \omega t, r\omega \cos \omega t)$$ $$\therefore \overrightarrow{v(t)}= (-r\omega \sin \omega t, r\omega \cos \omega t)　\cdots(ウ)$$ さらに、加速度を考えると、 $$\overrightarrow{a(t)}=\frac{d v(t)}{dt}$$ $$= (a_x(t), a_y(t))$$ $$= \left(\frac{d v_x(t)}{dt}, \frac{d v_y(t)}{dt} \right)$$ $$= (-r\omega^2 \cos \omega t, -r\omega^2 \sin \omega t)$$ $$\therefore \overrightarrow{a(t)}= (-r\omega^2 \cos \omega t, -r\omega^2 \sin \omega t)　\cdots(エ)$$ 以上より、
速度の大きさは $$\left| \overrightarrow{v(t)}\right| = \sqrt{(-r\omega\sin \omega t)^2+(r\omega\cos \omega t)^2}$$ $$\left|\overrightarrow{v(t)}\right| = \sqrt{(r\omega)^2\cdot(\sin^2 \omega t+\cos^2 \omega t)}$$ $$\therefore \left|\overrightarrow{v(t)}\right| = r\omega　\cdots(オ)$$
加速度の大きさは $$\left| \overrightarrow{a(t)}\right| = \sqrt{(-r\omega^2\sin \omega t)^2+(-r\omega^2\cos \omega t)^2}$$ $$\left|\overrightarrow{a(t)}\right| = \sqrt{(r\omega^2)^2\cdot(\sin^2 \omega t+\cos^2 \omega t)}$$ $$\therefore \left|\overrightarrow{a(t)}\right| = r\omega^2　\cdots(カ)$$ $\overrightarrow{r(t)}$ と $\overrightarrow{v(t)}$ の内積を計算すると、 $$\overrightarrow{r(t)}\cdot\overrightarrow{v(t)}= (r\cos\omega t)(-r\omega\sin \omega t) + (r\sin\omega t)(r\omega\cos \omega t)$$ $$\therefore \overrightarrow{r(t)}\cdot\overrightarrow{v(t)}= 0$$ これにより、
$\overrightarrow{r(t)}$ と $\overrightarrow{v(t)}$は直交し、速度ベクトルは、 「円の接線方向」になっていることがわかる。

また、$\overrightarrow{v(t)}$ と $\overrightarrow{a(t)}$ の内積を計算すると、 $$\overrightarrow{v(t)}\cdot\overrightarrow{a(t)}= (-r\omega\sin\omega t)(-r\omega^2\sin \omega t)$$ $$ + (r\omega\cos\omega t)(-r\omega^2\cos \omega t)$$ $$\therefore \overrightarrow{v(t)}\cdot\overrightarrow{a(t)}= 0$$ これにより、
$\overrightarrow{v(t)}$ と $\overrightarrow{a(t)}$は直交し、加速度ベクトルは、 「円の中心方向」になっていることがわかる。

ここで、質量mの質点Pが等速円運動しているとき、運動方程式は、 $$F = ma$$ (カ)により、 $$\therefore F= mr\omega^2　\cdots(キ)$$ この$F$を「向心力」といって、「円の中心向き」に働きます。

この「一定の向心力」のおかげで、「等速円運動になる」ことができます。