今回の話題は、「力学的エネルギーの導出過程」についてです。
では、始めましょう。
質量$m$の物体に時刻$t$の関数である外力$F(t)$が働いて$x$変位するとき、「運動方程式」は
$$m\cdot\frac{d^2x}{dt^2}=F(t) \cdots(ア)$$
で与えられることは既に解説済みである。
(ア)より、「合成微分」を適用して、 $$m\cdot\frac{dx}{dt}\cdot \frac{d}{dt} =F(t)\cdot \frac{dx}{dt}\cdot\frac{dt}{dx}$$ となり、 $$m\cdot\frac{dx}{dt}\cdot d\left(\frac{dx}{dt}\right) =F(t)\cdot \frac{dx}{dt}\cdot dt \cdots(イ)$$ であり、さらに$\dfrac{dx}{dt}=v$とおくと、 $$m\cdot v\cdot dv =F(t)\cdot dx$$ $$\int_{v(t_1)}^{v(t_2)} m\cdot v\cdot dv =\int_{x(t_1)}^{x(t_2)} F(t)\cdot dx \cdots(ウ)$$ ここで、$X = x(t)$とおくと、 $$\dfrac{dX}{dt}=\dfrac{d}{dt}\left(x(t)\right)$$ $$dX=d(x(t))$$ により、(ウ)は $$\int_{v(t_1)}^{v(t_2)} m\cdot v\cdot dv =\int_{x(t_1)}^{x(t_2)} F(t)\cdot dX$$ $$\int_{v(t_1)}^{v(t_2)} m\cdot v\cdot dv =\int_{X_1}^{X_2} F(X)\cdot dX$$ $$\Big[ \frac{1}{2}mv^2 \Big]_{v_1}^{v_2} = \int_{X_1}^{X_2} F(X)\cdot dX \cdots(エ)$$ ここで、右辺の$F(X)$は位置$X$の関数であるが、 「高校物理」では、通常、$F(X)=一定(定数)$として扱うので、単に「$F$」と表記すると、 $$\Big[ \frac{1}{2}mv^2 \Big]_{v_1}^{v_2} = \int_{X_1}^{X_2} F\cdot dX$$ $$\Big[ \frac{1}{2}mv^2 \Big]_{v_1}^{v_2} = \Big[FX\Big]_{X_1}^{X_2}$$ $$\frac{1}{2}{mv_2}^2-\frac{1}{2}{mv_1}^2 = F(X_2-X_1)$$ $$\therefore \frac{1}{2}{mv_2}^2-\frac{1}{2}{mv_1}^2 = F\cdot\Delta X \cdots(オ)$$ ここで、 $$\frac{1}{2}mv^2~~\Longrightarrow~「運動エネルギー」$$ $$F\cdot \Delta X~~\Longrightarrow~「外力Fのした仕事」$$ という。
結果(オ)の式の意味するところは、
外力$F$がする「仕事」は、「運動エネルギーを変化」させる
ということである。 ここで、外力$F$はベクトル量であり、「向きと大きさ」を持っている。ここでの$\Delta X$は、 「力の向きに移動した距離」である。
重力を例にとって考えると、力が一定、つまり大きさが一定で鉛直下方方向に働く場合
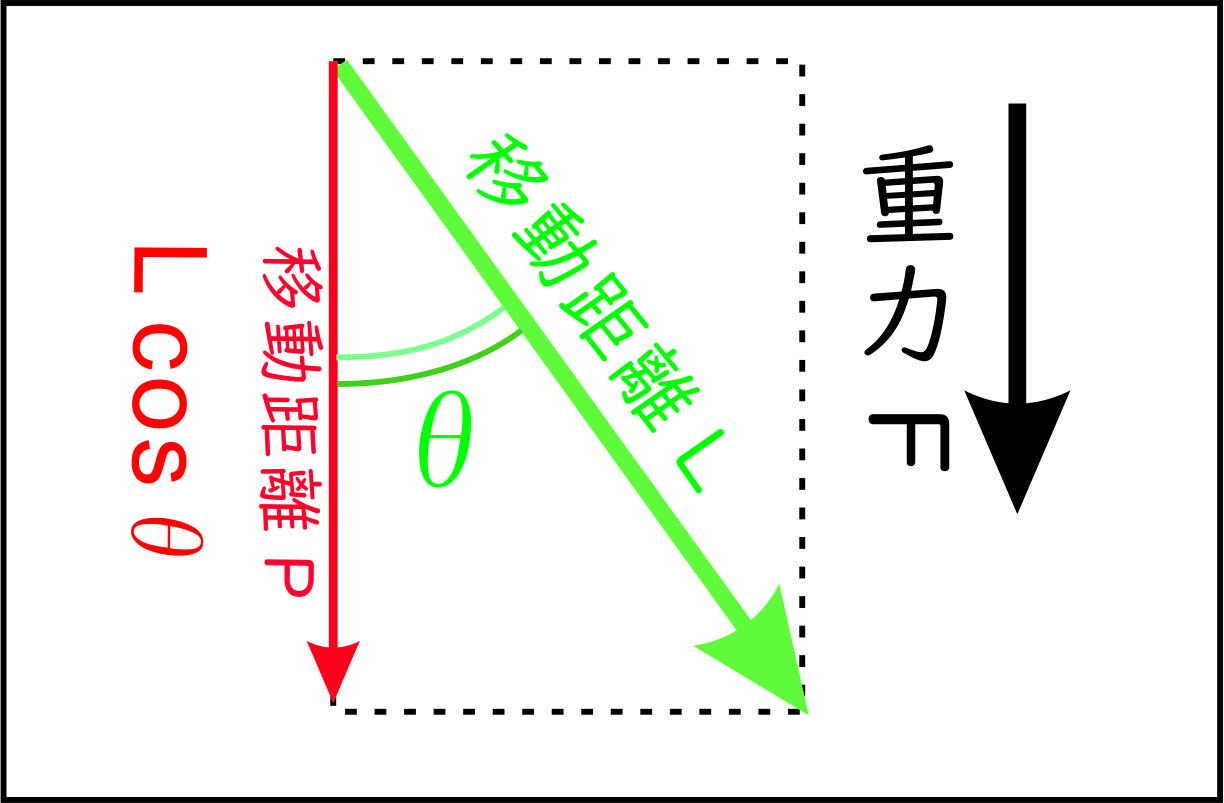
図の移動距離Lは「実際に移動した距離」であるが、先ほどの$\Delta X$ではない。
$\Delta X$は、重力F方向の成分である移動距離Pの「$L\cos \theta$」になる。注意してほしい。
また、重力$F$に対して垂直方向に移動した場合には、重力F方向の成分は0になるので、 $\Delta X =0$になる。つまり、重力がした仕事は0である。このことは重要である。気を付けよう。
一般に、物体を移動させるとき、物体に働く力がする仕事が、「途中の経路に無関係で始めと終わりの位置だけで決まる」場合 、その力を「保存力」という。重力、弾性力、万有引力、静電気力などは、保存力である。
$$保存力とは、つまり、外力の方向が常に変わらない力$$ のこと、
または $$往復の経路における仕事の和が0になる$$ ことである。たとえば、「摩擦力」は往復の経路を考えた場合に、同じ経路でも常に進行方向とは正反対の向きに摩擦力が作用するため、摩擦力がした仕事の総和は0にはならない。このとき、このような力を「非保存力」という。非保存力には他に「空気抵抗」などがある。
(ア)より、「合成微分」を適用して、 $$m\cdot\frac{dx}{dt}\cdot \frac{d}{dt} =F(t)\cdot \frac{dx}{dt}\cdot\frac{dt}{dx}$$ となり、 $$m\cdot\frac{dx}{dt}\cdot d\left(\frac{dx}{dt}\right) =F(t)\cdot \frac{dx}{dt}\cdot dt \cdots(イ)$$ であり、さらに$\dfrac{dx}{dt}=v$とおくと、 $$m\cdot v\cdot dv =F(t)\cdot dx$$ $$\int_{v(t_1)}^{v(t_2)} m\cdot v\cdot dv =\int_{x(t_1)}^{x(t_2)} F(t)\cdot dx \cdots(ウ)$$ ここで、$X = x(t)$とおくと、 $$\dfrac{dX}{dt}=\dfrac{d}{dt}\left(x(t)\right)$$ $$dX=d(x(t))$$ により、(ウ)は $$\int_{v(t_1)}^{v(t_2)} m\cdot v\cdot dv =\int_{x(t_1)}^{x(t_2)} F(t)\cdot dX$$ $$\int_{v(t_1)}^{v(t_2)} m\cdot v\cdot dv =\int_{X_1}^{X_2} F(X)\cdot dX$$ $$\Big[ \frac{1}{2}mv^2 \Big]_{v_1}^{v_2} = \int_{X_1}^{X_2} F(X)\cdot dX \cdots(エ)$$ ここで、右辺の$F(X)$は位置$X$の関数であるが、 「高校物理」では、通常、$F(X)=一定(定数)$として扱うので、単に「$F$」と表記すると、 $$\Big[ \frac{1}{2}mv^2 \Big]_{v_1}^{v_2} = \int_{X_1}^{X_2} F\cdot dX$$ $$\Big[ \frac{1}{2}mv^2 \Big]_{v_1}^{v_2} = \Big[FX\Big]_{X_1}^{X_2}$$ $$\frac{1}{2}{mv_2}^2-\frac{1}{2}{mv_1}^2 = F(X_2-X_1)$$ $$\therefore \frac{1}{2}{mv_2}^2-\frac{1}{2}{mv_1}^2 = F\cdot\Delta X \cdots(オ)$$ ここで、 $$\frac{1}{2}mv^2~~\Longrightarrow~「運動エネルギー」$$ $$F\cdot \Delta X~~\Longrightarrow~「外力Fのした仕事」$$ という。
結果(オ)の式の意味するところは、
外力$F$がする「仕事」は、「運動エネルギーを変化」させる
ということである。 ここで、外力$F$はベクトル量であり、「向きと大きさ」を持っている。ここでの$\Delta X$は、 「力の向きに移動した距離」である。
重力を例にとって考えると、力が一定、つまり大きさが一定で鉛直下方方向に働く場合

図の移動距離Lは「実際に移動した距離」であるが、先ほどの$\Delta X$ではない。
$\Delta X$は、重力F方向の成分である移動距離Pの「$L\cos \theta$」になる。注意してほしい。
また、重力$F$に対して垂直方向に移動した場合には、重力F方向の成分は0になるので、 $\Delta X =0$になる。つまり、重力がした仕事は0である。このことは重要である。気を付けよう。
一般に、物体を移動させるとき、物体に働く力がする仕事が、「途中の経路に無関係で始めと終わりの位置だけで決まる」場合 、その力を「保存力」という。重力、弾性力、万有引力、静電気力などは、保存力である。
$$保存力とは、つまり、外力の方向が常に変わらない力$$ のこと、
または $$往復の経路における仕事の和が0になる$$ ことである。たとえば、「摩擦力」は往復の経路を考えた場合に、同じ経路でも常に進行方向とは正反対の向きに摩擦力が作用するため、摩擦力がした仕事の総和は0にはならない。このとき、このような力を「非保存力」という。非保存力には他に「空気抵抗」などがある。
続いて、「位置エネルギーU」を考えていきましょう。
先ほどの(エ)において、$F\cdot \Delta X$は外力$F$のした仕事$W$であるが、
$$仕事はWは、「エネルギーそのもののカタチである」$$
という理解である。
というのは、たとえば、「重力位置エネルギー」を例にとると、
質量$m$の物体が静止した状態から、 重力に逆らって、極めてゆっくり、鉛直上方に距離$h$移動させた場合、 物体に対してした仕事は、 $$F\cdot \Delta X = mg \cdot h$$ であり、 よく知られた $$「重力位置エネルギー」= mgh$$ が示される。
「位置エネルギーU」は、
物体がその位置にあることで潜在的に持っているエネルギー
のことなので 、別名、「ポテンシャルエネルギー」とも言います。
というのは、たとえば、「重力位置エネルギー」を例にとると、
質量$m$の物体が静止した状態から、 重力に逆らって、極めてゆっくり、鉛直上方に距離$h$移動させた場合、 物体に対してした仕事は、 $$F\cdot \Delta X = mg \cdot h$$ であり、 よく知られた $$「重力位置エネルギー」= mgh$$ が示される。
「位置エネルギーU」は、
物体がその位置にあることで潜在的に持っているエネルギー
のことなので 、別名、「ポテンシャルエネルギー」とも言います。
いかがでしたか。理解出来ましたか。
次回にお会いしましょう。
では、また。