今回は、「電磁気」についての話題です。
では、さっそく、考えてみましょう。
「コンデンサーと電荷の移動」についてです。
問題
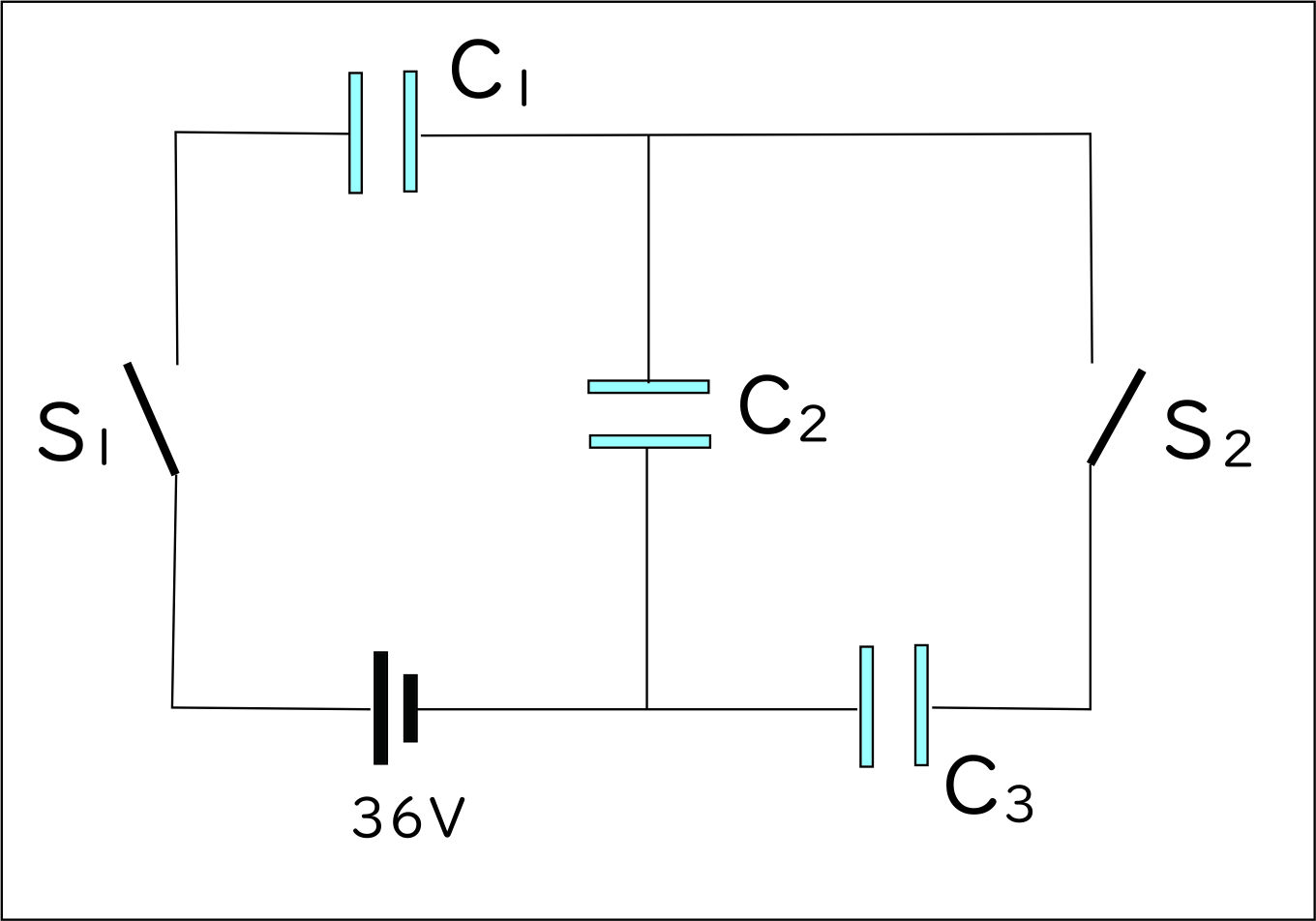
内部抵抗が無視できる起電力36V の電池と、3個のコンデンサー$C_1$(容量1$\mu F$)、$C_2$(容量1$\mu F$) 、$C_3$(容量2$\mu F$)、およびスイッチ$S_1$、$S_2$を図のように接続した。 最初、スイッチは2つとも開いており、3個のコンデンサーすべてに電荷は蓄えられていないとする。

内部抵抗が無視できる起電力36V の電池と、3個のコンデンサー$C_1$(容量1$\mu F$)、$C_2$(容量1$\mu F$) 、$C_3$(容量2$\mu F$)、およびスイッチ$S_1$、$S_2$を図のように接続した。 最初、スイッチは2つとも開いており、3個のコンデンサーすべてに電荷は蓄えられていないとする。
- まず、$S_1$を閉じた。このとき$C_1$に蓄えられる電荷と$C_2$に蓄えられる電荷はそれぞれいくらか。
- 次に$S_1$を開き、$S_2$を閉じる。このとき、$C_2$に蓄えられていた電荷は放電され、 $C_3$が充電される。十分時間がたった後、$C_2$と$C_3$に蓄えられる電荷はそれぞれいくらか。
- 続いて、$S_2$を開き、$S_1$を閉じた。十分時間がたったとき、 $C_1$、$C_2$に蓄えられる電荷はそれぞれいくらか。
- 再び$S_1$を開き、$S_2$を閉じる。十分時間がたったとき、$C_2$、$C_3$に蓄えられる電荷は それぞれいくらか。
- (3)、(4)の操作を無限に繰り返して行ったとき、$C_1$、$C_2$、$C_3$に蓄えられる電荷はそれぞれいくらか。
- $C_1$と$C_2$の容量が同じで直列接続なので、それぞれのコンデンサーに18Vずつ 電圧が加わるからどちらも同じ電荷$Q$が蓄えられて、 $$\therefore Q=1\times18=18\mu C \cdots(ア) //$$
- $C_2$と$C_3$の並列接続なので電位差が等しく、それぞれの電気量を$Q_2~[\mu C]$、$Q_3~[\mu C]$ とすると、 $$\frac{Q_2}{C_2}=\frac{Q_3}{C_3}$$ $$\frac{Q_2}{1}=\frac{Q_3}{2}$$ $$\therefore Q_2=\frac{Q_3}{2} \cdots(イ)$$ また、電気量保存より、(ア)とあわせて、 $$Q=Q_2+Q_3$$ $$\therefore Q_2+Q_3=18 \cdots(ウ)$$ (イ)を(ウ)に代入して、 $$\frac{Q_3}{2}+Q_3=18$$ $$\frac{3}{2}Q_3=18$$ $$\therefore Q_3 = 12 \mu C //$$ これを(イ)に代入して、 $$C_2 = \frac{12}{2}$$ $$\therefore C_2 = 6 \mu C //$$
-
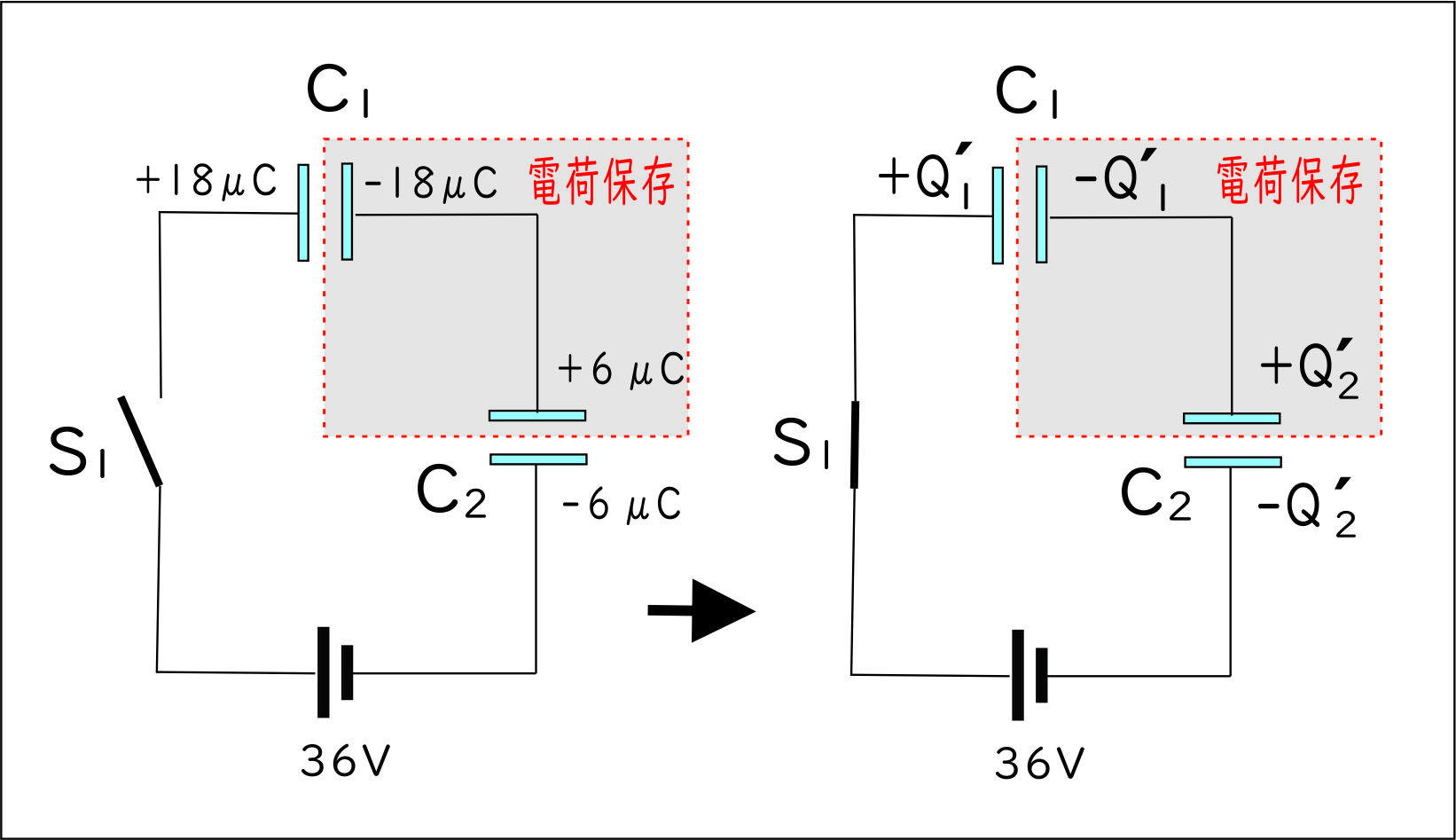
$S_1$を閉じた後、$C_1$と$C_2$の電位差が$V_1$[V]、$V_2$[V]、電気量が$Q_1'$、$Q_2'$になったとすると、 $$Q_1'=C_1V_1、Q_2'=C_2V_2$$ $$Q_1'=1\cdot V_1、Q_2'=1\cdot V_2$$ $$Q_1'=V_1、Q_2'=V_2 \cdots(エ)$$ また、電気量保存より $$-18+6=-Q_1'+Q_2'=-C_1V_1+C_2V_2$$ $$-12=-1\cdot V_1+ 1\cdot V_2$$ $$\therefore -12=- V_1+ V_2 \cdots(オ)$$ 電位差の関係より、 $$\therefore 36=V_1+V_2 \cdots(カ)$$ (オ)、(カ)より、 $$\therefore V_1=24~[V]、V_2=12~[V]$$ よって、 $$\therefore Q_1'=C_1V_1=1\cdot 24=24~[\mu F] //$$ $$\therefore Q_2'=C_2V_2=1\cdot 12 = 12~[\mu F] //$$ - $S_1$を開いて$S_2$を閉じる前の$C_1$、$C_2$の電荷はそれぞれ$12\mu C$、$12 \mu C$であるから、 (2)と同様にして、 $$Q_2'' = 8~[\mu C]$$ $$Q_3'' = 16~[\mu C]$$
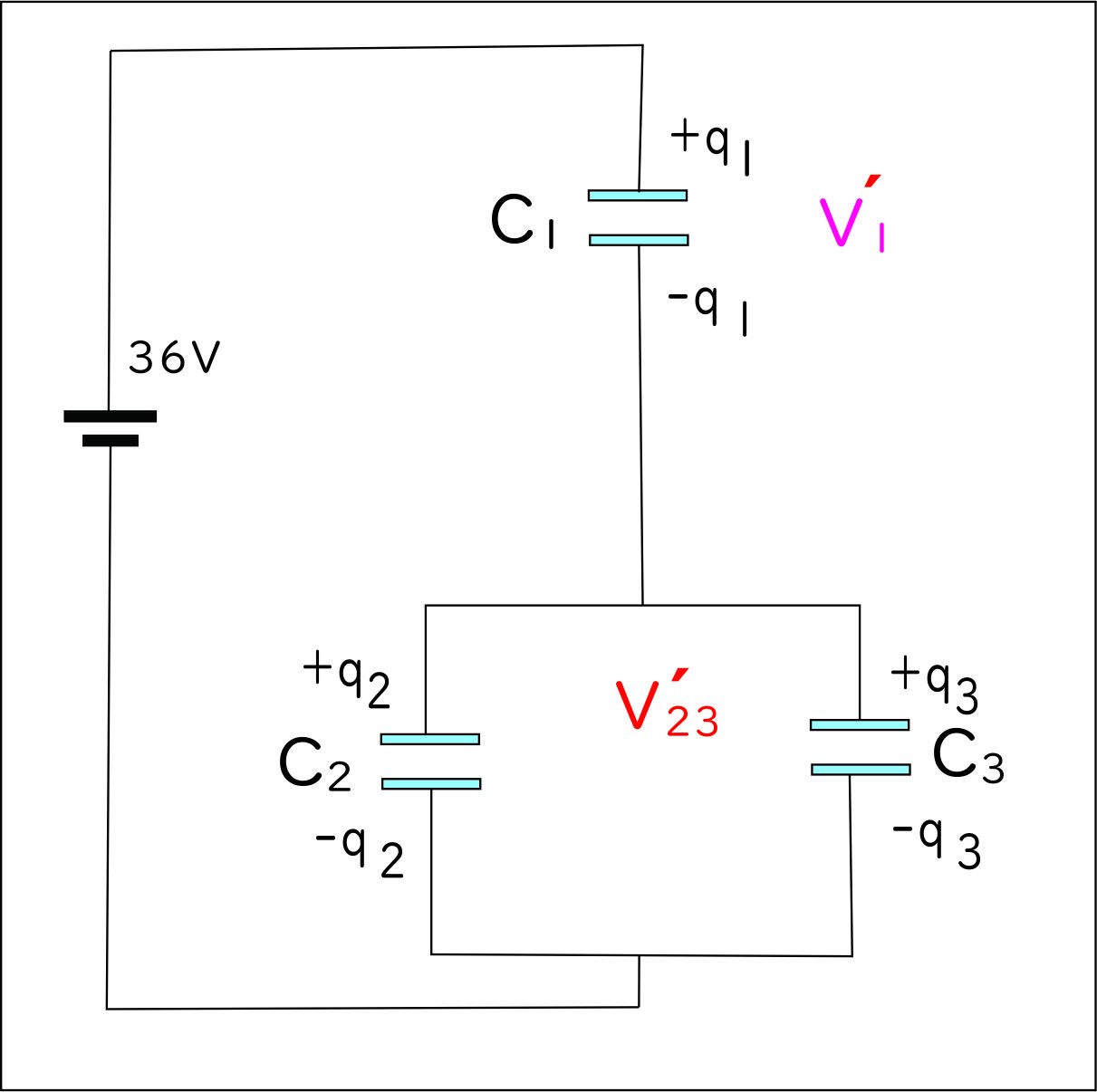
- このスイッチ$S_1$、$S_2$の開閉の操作は、
$C_2$に蓄えられた電荷を少しずつ$C_3$に分配していくことなるので、
操作を無限に繰り返したあとは、図のような回路のコンデンサーに充電したのと同じことになる。
いかがでしたか。
理解は出来ましたか?
では、また次回にお会いしましょう。