今回は、『運動方程式』がテーマで「導出過程」を見ていくことにする。 エネルギーの導出は別の機会に書いていこうと思います。
では、始めてみよう。
$$質量mの物体に力Fが加わって、加速度aが生じる \cdots(ア)$$
この因果関係は、大変重要である。けして、「加速度が生まれてから力が加わるのではない」ので、注意しよう。
ここで、静止している質量$m$の物体を移動させるには、外力$F$が必要である。 そして、変位$x$は、外力$F$が大きければ大きいほど変位は大きくなる。 $$変位xは、外力Fに比例する \cdots(イ)$$ また、質量$m$の大きさが大きいほど、変位は小さい。 このことから、 $$変位xは、質量mに反比例する \cdots(ウ)$$ ことが言え、(イ)、(ウ)から、 $$x \propto \frac{F}{m}$$ $$x = k\times \frac{F}{m}$$ とおける。ここで、$\dfrac{k}{m}=\dfrac{1}{M}$とおく。また、 $$質量mが決まると、変位xが決まる$$ わけだが、この場合、物体が移動している間に「質量は一定」である、と考えてよいので、 $$外力Fは時刻tに依存すると考えられる$$ つまり、外力$F$は時間の関数$f(t)$とおける。 $$x=\frac{1}{M}\cdot f(t)$$ このとき、ある時刻0から時刻$t$まで経過したときの「変化の割合」をかんがえてみると、 $$\dfrac{\Delta x}{\Delta t} = \frac{1}{M}\cdot \dfrac{\Delta f(t)}{\Delta t}$$ ここで、時刻$t$を限りなく時刻0に近づけてみる、つまり、時間を0に近づけてみることを考える。 $$\lim_{\Delta t \to0}\dfrac{\Delta x}{\Delta t} = \lim_{\Delta t\to0}\frac{1}{M}\cdot \dfrac{\Delta f(t)}{\Delta t}$$ $$\dfrac{dx}{dt} =\frac{1}{M}\cdot \dfrac{d\{ f(t)\}}{dt}$$ $$\dfrac{dx}{dt} = \frac{1}{M}\cdot f'(t)$$ $$\dfrac{d^2x}{dt^2} = \frac{1}{M}\cdot f''(t) \cdots (エ)$$ ここで、$\dfrac{d^2x}{dt^2}= a(t)$($a(t)$は「加速度」)、$f''(t)=F(t)$とおけば、(エ)より、 $$a(t)=\frac{F(t)}{M} \cdots(オ)$$ $$F(t)=M\cdot a(t) \cdots(カ)$$ となる。
ここで、高校物理では、通常、「加速度が一定である運動」を扱うので、$a(t)=a$、$F(t)=F$として考えれば、 教科書レベルでお馴染みの「運動方程式」 $$F=Ma \cdots(キ)$$ に記述できる。たとえば、「加速度が一定でない運動として、『等速円運動』」がある。 速さは一定だけど、向きが刻々と変化する。つまり、速度は変化する。 けして、「等速度円運動とは言わない」ので、注意してほしい。等速度と言ってしまったら、向きも大きさも変わらないことを意味して、 「等速直線運動」になってしまう。円運動にはならない。
この因果関係は、大変重要である。けして、「加速度が生まれてから力が加わるのではない」ので、注意しよう。
ここで、静止している質量$m$の物体を移動させるには、外力$F$が必要である。 そして、変位$x$は、外力$F$が大きければ大きいほど変位は大きくなる。 $$変位xは、外力Fに比例する \cdots(イ)$$ また、質量$m$の大きさが大きいほど、変位は小さい。 このことから、 $$変位xは、質量mに反比例する \cdots(ウ)$$ ことが言え、(イ)、(ウ)から、 $$x \propto \frac{F}{m}$$ $$x = k\times \frac{F}{m}$$ とおける。ここで、$\dfrac{k}{m}=\dfrac{1}{M}$とおく。また、 $$質量mが決まると、変位xが決まる$$ わけだが、この場合、物体が移動している間に「質量は一定」である、と考えてよいので、 $$外力Fは時刻tに依存すると考えられる$$ つまり、外力$F$は時間の関数$f(t)$とおける。 $$x=\frac{1}{M}\cdot f(t)$$ このとき、ある時刻0から時刻$t$まで経過したときの「変化の割合」をかんがえてみると、 $$\dfrac{\Delta x}{\Delta t} = \frac{1}{M}\cdot \dfrac{\Delta f(t)}{\Delta t}$$ ここで、時刻$t$を限りなく時刻0に近づけてみる、つまり、時間を0に近づけてみることを考える。 $$\lim_{\Delta t \to0}\dfrac{\Delta x}{\Delta t} = \lim_{\Delta t\to0}\frac{1}{M}\cdot \dfrac{\Delta f(t)}{\Delta t}$$ $$\dfrac{dx}{dt} =\frac{1}{M}\cdot \dfrac{d\{ f(t)\}}{dt}$$ $$\dfrac{dx}{dt} = \frac{1}{M}\cdot f'(t)$$ $$\dfrac{d^2x}{dt^2} = \frac{1}{M}\cdot f''(t) \cdots (エ)$$ ここで、$\dfrac{d^2x}{dt^2}= a(t)$($a(t)$は「加速度」)、$f''(t)=F(t)$とおけば、(エ)より、 $$a(t)=\frac{F(t)}{M} \cdots(オ)$$ $$F(t)=M\cdot a(t) \cdots(カ)$$ となる。
ここで、高校物理では、通常、「加速度が一定である運動」を扱うので、$a(t)=a$、$F(t)=F$として考えれば、 教科書レベルでお馴染みの「運動方程式」 $$F=Ma \cdots(キ)$$ に記述できる。たとえば、「加速度が一定でない運動として、『等速円運動』」がある。 速さは一定だけど、向きが刻々と変化する。つまり、速度は変化する。 けして、「等速度円運動とは言わない」ので、注意してほしい。等速度と言ってしまったら、向きも大きさも変わらないことを意味して、 「等速直線運動」になってしまう。円運動にはならない。
次に、「運動量と力積」の話題です。
2つ以上の物体が衝突において、「衝突の瞬間」の力の作用は「作用反作用」によって、「運動方程式」(上記の(カ))
により考えることは可能である。しかし、「衝突の時間的変化」を考えることができない。
そこで、「及ぼしあう力の時間的変化」を考えてみる。
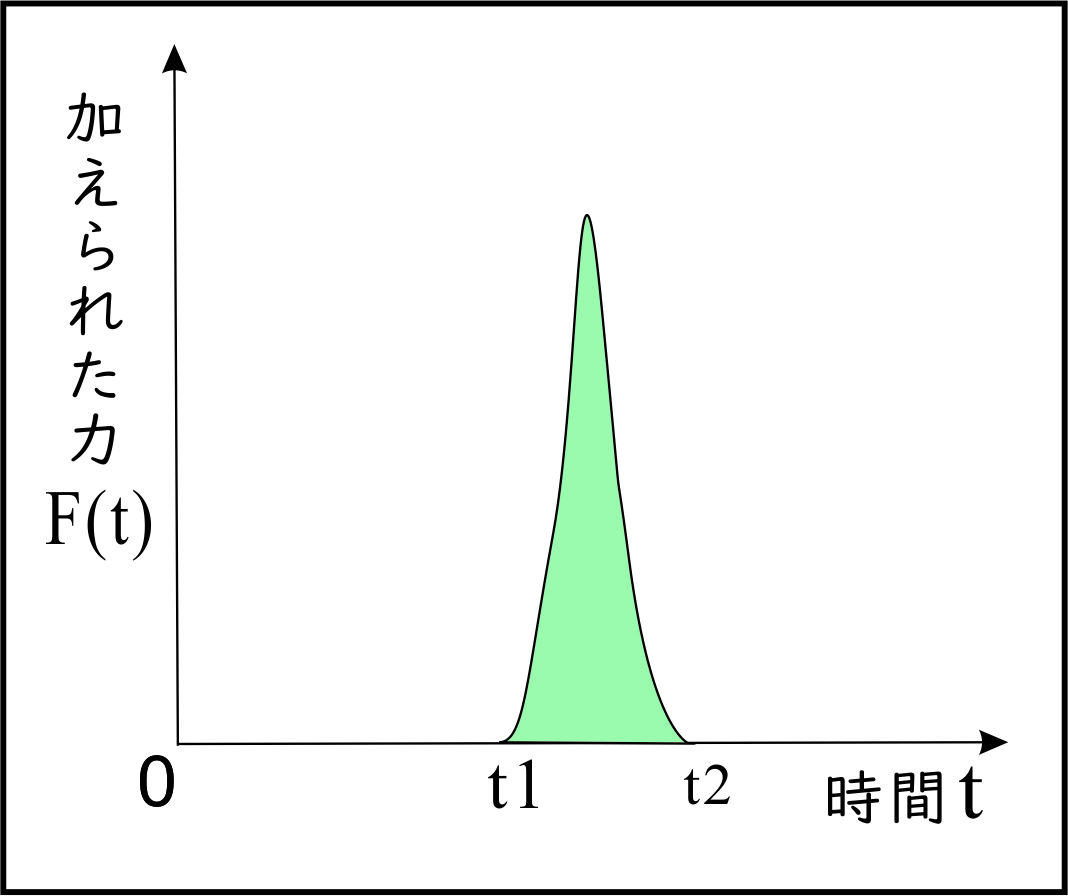
上記(カ)の式を時間$t$で積分することを考える。つまり、上図の緑の領域の面積を考える。 $$F(t)=M\cdot a(t)$$ $$\int_{t_1}^{t_2}F(t)dt=\int_{t_1}^{t_2}M\cdot a(t)dt$$ $$\int_{t_1}^{t_2}F(t)dt=\int_{t_1}^{t_2}M\cdot \frac{d^2x}{dt^2}dt$$ $$\int_{t_1}^{t_2}F(t)dt=\int_{t_1}^{t_2}M\cdot \frac{dv}{dt}dt$$ $$\int_{t_1}^{t_2}F(t)dt=\int_{v(t_1)}^{v(t_2)}M\cdot dv \cdots(ク)$$ ここで、高校物理では、直接$F(t)$を扱わないで、時間($t_1$~$t_2$)における 「力の平均値$\overline{F_0(t)}~(=\overline{F_0}=(定数))$」を考えて、

薄紫色の領域の面積を考える。これは長方形の面積なので簡単に求めることができる。
(ク)より、 $$\int_{t_1}^{t_2}\overline{F_0}dt=\int_{v(t_1)}^{v(t_2)} dv \cdots(ケ)$$ $$\Big[\overline{F_0}\cdot t\Big]_{t_1}^{t_2} =\Big[Mv\Big]_{v(t_1)}^{v(t_2)} $$ $$\overline{F_0}\cdot(t_2-t_1) = Mv_2-Mv_1$$ $$\overline{F_0}\cdot\Delta t = Mv_2-Mv_1 \cdots(コ)$$ ここで、 $$Mv~を運動量、~F\cdot\Delta t~を力積$$ と言う。
そこで、「及ぼしあう力の時間的変化」を考えてみる。

上記(カ)の式を時間$t$で積分することを考える。つまり、上図の緑の領域の面積を考える。 $$F(t)=M\cdot a(t)$$ $$\int_{t_1}^{t_2}F(t)dt=\int_{t_1}^{t_2}M\cdot a(t)dt$$ $$\int_{t_1}^{t_2}F(t)dt=\int_{t_1}^{t_2}M\cdot \frac{d^2x}{dt^2}dt$$ $$\int_{t_1}^{t_2}F(t)dt=\int_{t_1}^{t_2}M\cdot \frac{dv}{dt}dt$$ $$\int_{t_1}^{t_2}F(t)dt=\int_{v(t_1)}^{v(t_2)}M\cdot dv \cdots(ク)$$ ここで、高校物理では、直接$F(t)$を扱わないで、時間($t_1$~$t_2$)における 「力の平均値$\overline{F_0(t)}~(=\overline{F_0}=(定数))$」を考えて、

薄紫色の領域の面積を考える。これは長方形の面積なので簡単に求めることができる。
(ク)より、 $$\int_{t_1}^{t_2}\overline{F_0}dt=\int_{v(t_1)}^{v(t_2)} dv \cdots(ケ)$$ $$\Big[\overline{F_0}\cdot t\Big]_{t_1}^{t_2} =\Big[Mv\Big]_{v(t_1)}^{v(t_2)} $$ $$\overline{F_0}\cdot(t_2-t_1) = Mv_2-Mv_1$$ $$\overline{F_0}\cdot\Delta t = Mv_2-Mv_1 \cdots(コ)$$ ここで、 $$Mv~を運動量、~F\cdot\Delta t~を力積$$ と言う。