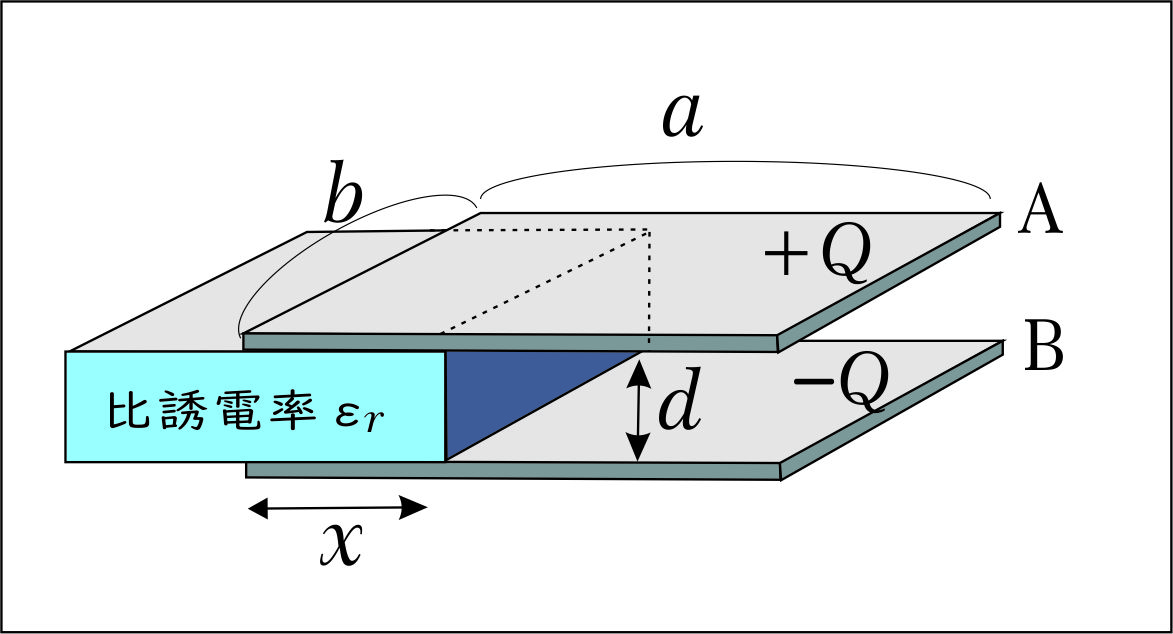
まず、図のコンデンサー容量を考えてみよう。

誘電体 ( 比誘電率$\epsilon_r~$) を含む部分のコンデンサー容量$C_1$は $$C_1 = \epsilon_0\epsilon_r\frac{bx}{d}$$ 誘電体を含まない部分のコンデンサー容量$C_2$は $$C_2 = \epsilon_0\frac{(a-x)b}{d}$$ よって、$C_1$と$C_2$の合成容量$C$は、並列と考えて $$C=C_1+C_2$$ $$C=\epsilon_0\epsilon_r\frac{bx}{d} + \epsilon_0\frac{(a-x)b}{d}$$ $$C=\frac{\epsilon_0\epsilon_r\cdot bx + \epsilon_0(a-x)b}{d}$$ $$\therefore　C=\frac{\epsilon_0b}{d}(a+(\epsilon_r-1)x)　\cdots(ア)$$ また、静電エネルギー$U$は、 $$U = \frac{Q^2}{2C}$$ $$\therefore　U = \frac{Q^2d}{2\epsilon_0b(a+(\epsilon_r-1)x)}　\cdots(イ)$$ となる。

ここで、外力$F$ を右方向(内部方向)に加えて、誘電体をコンデンサーの内部に移動させたとしたら、 外力のした仕事は正であり、その分$U$は増加するはずだが、（イ）の結果より、 $U$は減少しているので、矛盾する。 つまり、外力は左向きに加えたことになる。

このことから、 ことがわかる。