コンデンサー容量について考えてみよう。
前回の話の中で、
平行板コンデンサーにおいて、 極板面積 $S$ 、間隔 $d$ であるとすると、 であることは説明した。

まず、コンデンサー内に「導体」を含ませたときを考えよう。


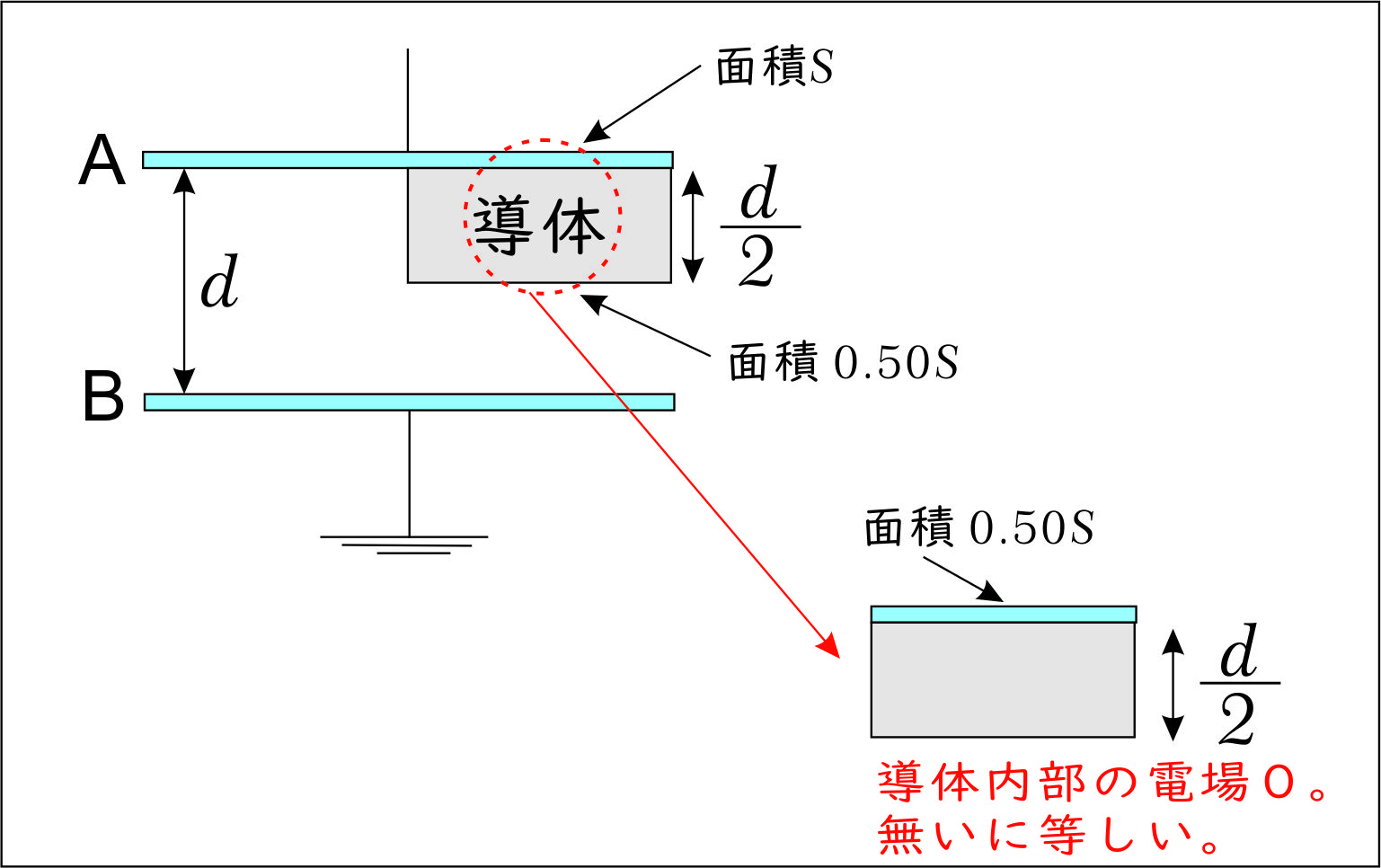
上図において、導体部分については、極版に電荷が与えられると になる。結局、下図のようなコンデンサー構造になる。


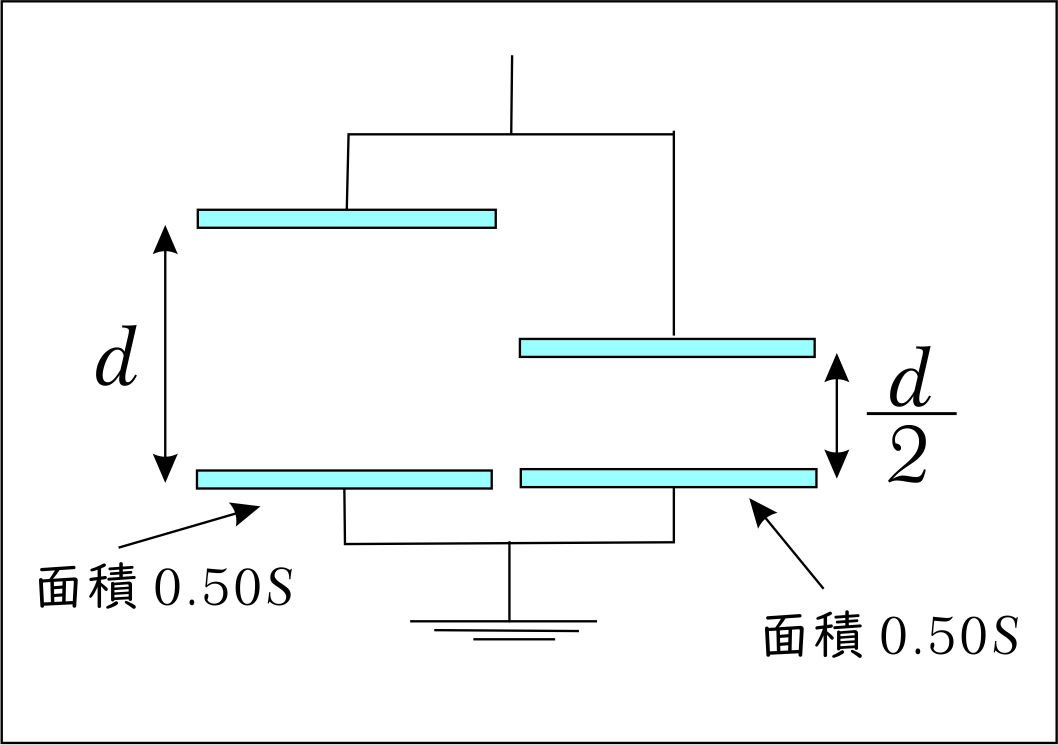
(ア)により、元のコンデンサー容量を $C$ とすると、

左部分について、極板面積 $0.50S$、間隔 $d$ のコンデンサー容量$C_1$ は、 $$C_1 = C \times 0.50\times 1.0=\frac{1}{2}C$$ 右部分について、極板面積 $0.50S$、間隔 $\dfrac{1}{2}d$ のコンデンサー容量$C_2$ は、 $$C_2 = C \times 0.50\times \dfrac{1}{\dfrac{1}{2}}=C$$ $C_1$と$C_2$の合成容量 $C_Z$ は、「並列」で、 $$C_Z=C_1+C_2$$ $$C_Z=\frac{1}{2}C+C$$ $$\therefore　C_Z=\frac{3}{2}C　//$$

つぎに、コンデンサー内に「誘電体(比誘電率 $\epsilon$ )」を含ませたときを考えよう。


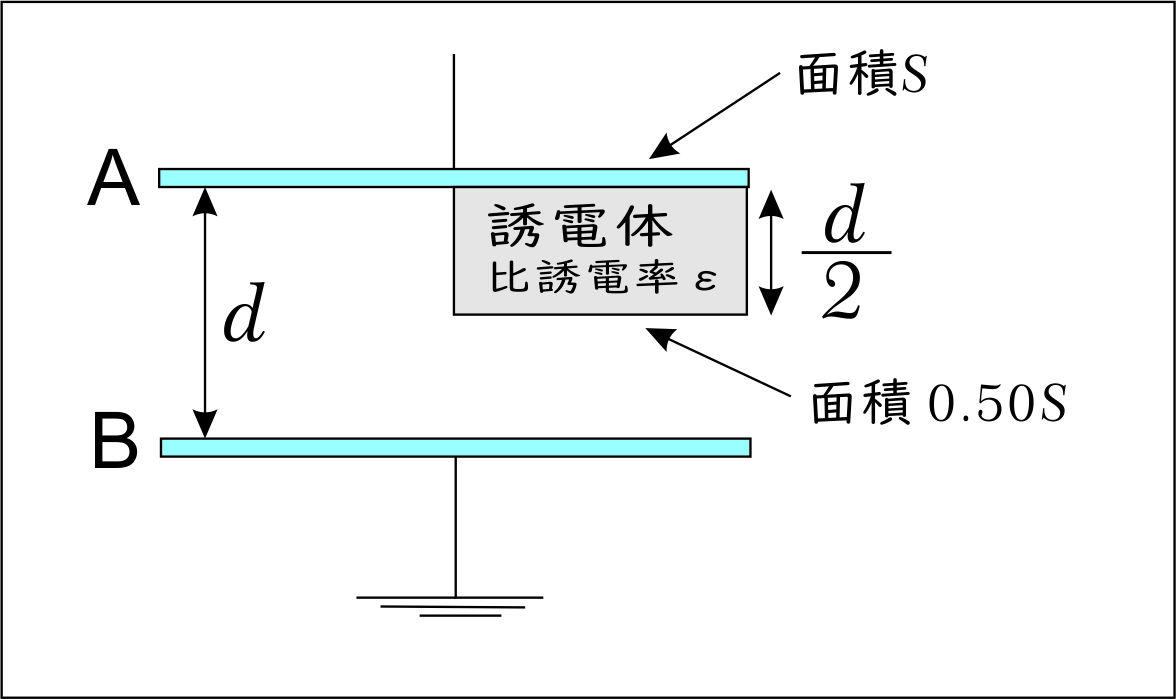
このとき、コンデンサーの構造は以下の図のようなコンデンサー構造に分割して考えることができる。


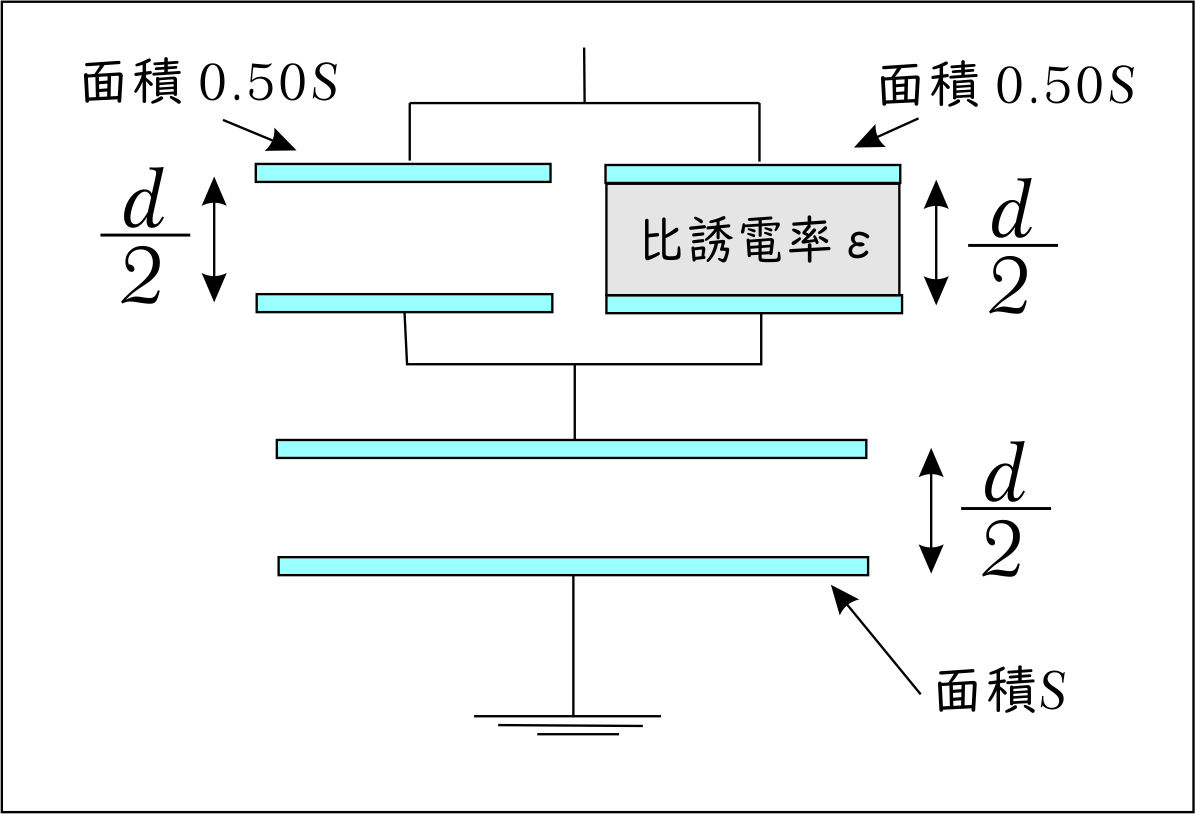
まず、左上の誘電体を含んでいない部分の容量 $C_1$ は、
極板面積 $0.50S$、間隔 $\dfrac{1}{2}d$ のコンデンサー容量$C_1$ より、 $$C_1 = C \times 0.50\times \dfrac{1}{\dfrac{1}{2}}=C$$ つぎに、右上の誘電体を含む部分の容量 $C_2$ は、
極板面積 $0.50S$、間隔 $\dfrac{1}{2}d$ のコンデンサー容量$C_1$ より、 真空中の誘電率を$\epsilon_0$とすると $$比誘電率 \epsilon = \frac{\epsilon_r}{\epsilon_0} $$ なので $$誘電率 \epsilon_r = \epsilon\epsilon_0$$ である。 $$C_2 = \frac{\epsilon_r}{\epsilon_0} \cdot C \times 0.50\times \dfrac{1}{\dfrac{1}{2}}=\epsilon \cdot C$$ さらに、下部分のコンデンサー容量 $C_3$ は、 極板面積 $1.0S$、間隔 $\dfrac{1}{2}d$ のコンデンサー容量$C_3$ より、 $$C_3 = C \times 1.0 \times \dfrac{1}{\dfrac{1}{2}}=2C$$ である。

$C_1$と$C_2$は「並列」なので、合成容量$C_X$は、 $$C_X = C_1+C_2$$ $$C_X = C + \epsilon \cdot C $$ $$C_X = (1+\epsilon)C$$ この合成コンデンサー容量$C_X$とコンデンサー容量 $C_3$ とは「直列」結合より、 合成容量 $C_Y$ は、 $$\frac{1}{C_Y} = \frac{1}{C_X}+\frac{1}{C_3}$$ $$\frac{1}{C_Y} = \frac{1}{(1+\epsilon)C}+\frac{1}{2C}$$ $$\frac{1}{C_Y} = \frac{2 + (1+\epsilon)}{2(1+\epsilon)C}$$ $$\frac{1}{C_Y} = \frac{3+\epsilon}{2(1+\epsilon)C}$$ $$\therefore　C_Y = \frac{2(1+\epsilon)}{3+\epsilon}C　//$$