今回は、「電磁気」についての話題です。
では、さっそく、考えてみましょう。
「コンデンサー」についてです。
前回までの話で、「1平板」の導体では、片面電界 $E$ は
片面の電界 $E~~=~~\dfrac{Q}{2\epsilon_0S}~~[\mathrm{~N/C~}] \cdots(ア)$
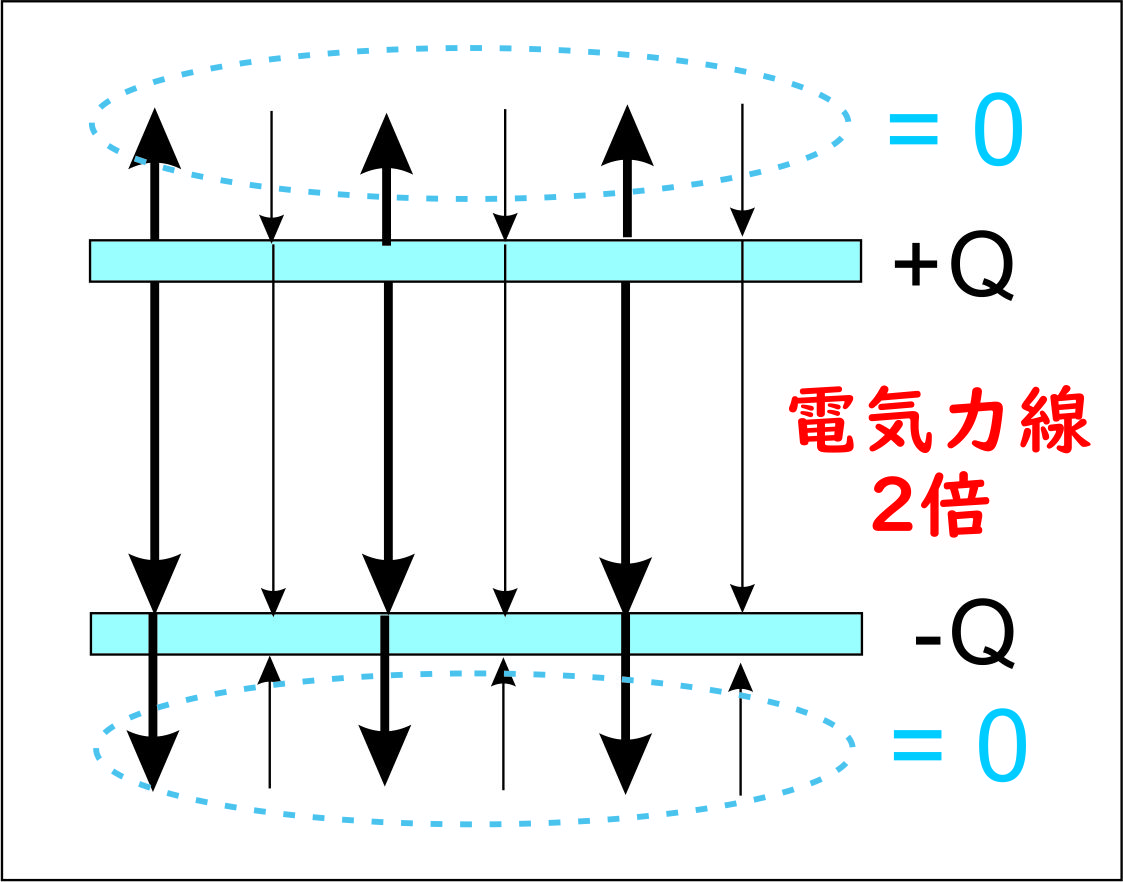
ここで、「2平板」にすることを考える。一方の平板に $+Q~~[~\mathrm{C}~]$、他方の平板に $-Q~~[~\mathrm{C}~]$ 与えた「コンデンサー」を考えると、「電気力線」によれば、
【重ね合わせの原理】により、両極板間では【力線密度2倍】で、外部 = 0
つまり、(ア)より、 $$E' = 2E$$
コンデンサー内部の電界 $E' = \dfrac{Q}{\epsilon_0 S}~~~[\mathrm{~N/C~}] \cdots(イ)$
$C=\dfrac{Q}{V}=\epsilon_0\dfrac{S}{ d}~~~[~\mathrm{F}~] \cdots(ウ)$
コンデンサー容量$C$ は、極板面積 $S$ に比例し、極板間隔 $d$ に反比例する
コンデンサーのエネルギーについて考えよう。
いま、極板Aの電荷が $+q$、極板Bの電荷が $-q$ になっているとする。
このときのAB間の電位差 $V(q)$ は(ウ)式より、 $$V(q) = \frac{q}{C} \cdots(エ)$$ このとき、微小電荷$\Delta q$ を極板Bから極板Aまで、静電気力に逆らって、 ゆっくり移動させることを考える。そうすると、外力がする仕事 $\Delta W$ は、 $\Delta q$ が十分小さければ、AB間の電位差 $V(q)$ を一定とみなせるので、 $$\Delta W = V(q) \cdot\Delta q$$ と表せる。(エ)より、 $$\Delta W = \frac{q}{C}\cdot \Delta q$$ $$W=\int_0^Q V(q)dq$$ $$=\frac{1}{C}\int_0^Q q~~ dq$$ $$=\frac{1}{C}\left[\frac{q^2}{2}\right]_0^{Q}$$
$W = \dfrac{Q^2}{2C}$
$U = \dfrac{Q^2}{2C}=\dfrac{1}{2}QV=\dfrac{1}{2}CV^2 \cdots(オ)$
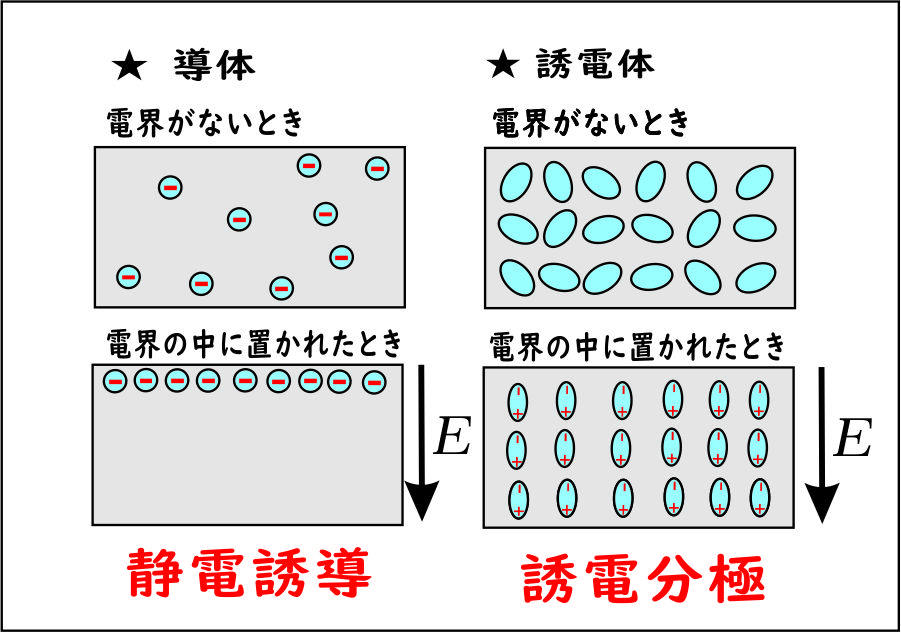
すべての物質は「導体」と「誘電体(不導体)」に分けられる。 「導体」は言うまでもなく、「自由電子 $e^{-}$ が担い手」となって、通電性がある。導体が電場内に置かれると、 導体内部で自由電子が移動して、自由電子が一方に偏り、結果として、導体に極性が生じる。これを「静電誘導」という。 一方の「誘電体(不導体)」は 自由電子をもたないので電気を通さない。誘電体においては、電場の中に置かれると、「原子内部で電子曇の偏りができる」 (電子は原子から飛び出すことができない)ので、 原子レベルで、$+極$、$-極$のように極性が生じる。このことを「誘電分極」という。
誘電体をコンデンサー内部に含ませると、
誘電分極による絶縁体内の電場が空間部の $\dfrac{1}{\epsilon}$ 倍となる
真空中に対する絶縁体の誘電率 $\epsilon_r$ を「比誘電率 $\epsilon_r=\dfrac{\epsilon}{\epsilon_0}$ ($\epsilon_0 < \epsilon$) 」という
コンデンサーの連結を考えよう。「抵抗の連結」とは逆になっている。
[ 1 ] 直列
$$\frac{1}{C}=\frac{1}{C_1}+\frac{1}{C_2}+\cdots+\frac{1}{C_n}$$ $$Q=Q_1 = Q_2 =\cdots + Q_n$$
[ 2 ] 並列
$$C=C_1+C_2+ \cdots + C_n$$ $$Q=\frac{C}{C_1+C_2+\cdots + C_n}$$
いかがでしたか。
理解は出来ましたか?
では、また次回にお会いしましょう。