今回は、「電磁気」についての話題です。
では、さっそく、考えてみましょう。
「電界と電位」についてです。
金属球に電荷 $q$ を与えると、
電荷は「金属表面に一様に分布」する $\cdots(ア)$
このとき、
導体内部には「電荷・電荷なし」 $\cdots(イ)$
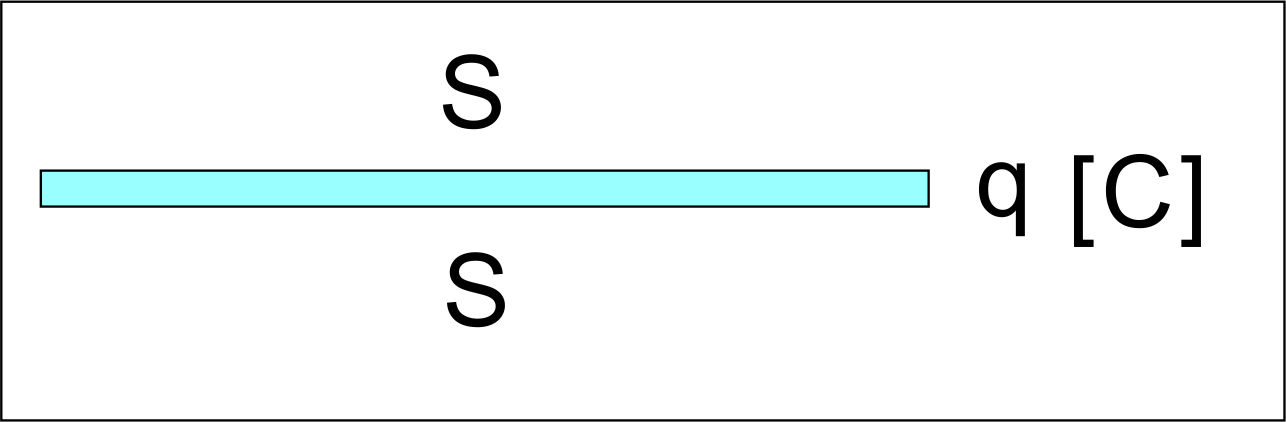
いま、「平面板の導体」を考える。片面の面積を $S$ とし、厚さは無視できるとする。 この平面板に電荷 $q$ を与えると、「導体の表面に一様に電荷 $q$ が分布する」ことから、
片面の電気量($q$)$~~=~~\dfrac{Q}{2S}~~[\mathrm{C/m^2}]$
$電界~E~~=~~\dfrac{4\pi k Q}{2S} \cdots(ウ)$
平面板の片面がつくり出す電界 $E$
を表している。ここで、
真空の誘電率 $\epsilon_0 ~~=~~\dfrac{1}{4\pi k} \cdots(エ)$
$電界~E~~=~~\dfrac{Q}{2\epsilon_0 S} \cdots(オ)$
「電位」とは、「単位電荷」が、ある位置に持つ「位置エネルギー」のことである。
「位置エネルギー」= 「外力に逆らってした仕事 」なので、
電位 V は$~~+1~(~\mathrm{C}~)$ の電荷を基準点P$_0$ から点P まで逆らって 運ぶのに要する仕事 V (J)
つまり、電荷 $q$ に対しての仕事を $W$ とすると、
$V~=~\dfrac{W}{q}$
$\therefore$ $U=qV~~[~\mathrm{J}~]$ $\cdots(カ)$
電位差 $=$ 電圧
基準点の選び方で「電位の値は変動」する
普 通 $\longrightarrow$ 【アース】の電位を0
点電荷 $\longrightarrow$ 【無限遠】の電位を0
(カ)より、 $$W = qV \cdots(キ)$$ 一方で、電界の定義より $$E=\frac{F}{q} ~~[~\mathrm{N/C}~]$$ だから、 $$W= (~qE~)\cdot d \cdots(ク)$$ $(キ)~ =~ (ク)~~$ より、 $$qV~ = ~(~qE~)\cdot d $$ これより、「電界と電位差との関係」は、
$\therefore V~=~dE~~~[~\mathrm{V}~]$ $\cdots(ケ)$
点電荷電荷のまわりの点の電位は、 $$V = \Sigma ~~k\dfrac{q}{r^2}\Delta~=~\int_r^{\infty}k\dfrac{q}{x^2}dx$$ $$=\left[-k\frac{q}{x}\right]_r^{\infty}$$ $$= k\frac{q}{r}$$
$\therefore V~=~k~~\dfrac{q}{r}~~~[~\mathrm{V}~]$ $\cdots(コ)$
いかがでしたか。
理解は出来ましたか?
では、また次回にお会いしましょう。