真空中で、距離 $r$ だけ離れた、電気量 $q_1$、$q_2$ を持った２つの点電荷の間には、 という力がはたらくことが知られている。これを「クーロンの法則」という。
ただし、$8.99\times10^9~~[\mathrm{Nm^2/C}]$。

「万有引力の法則」ととても似ているが、万有引力が常に引力であるのに対し、 クーロン力は同じ符号のとき「斥力」、異符号のとき「引力」としてはたらくのが大きな違いである。

電荷 $q$ があれば、それによって「電場」という「場」が作られる。

ここで、「電場」を として、定義する。
つまり、電場 $E$ は と定義できる。 (ウ)に(ア)を代入して $$E = \frac{k_0\dfrac{qq_2}{r^2}}{q_2}$$ これは、「点電荷 $q$ が中心から $r$ の位置に作り出す電界 $E$ 」を表す。

ところで、電場は「向きと大きさ」を持つ「ベクトル量」であり、その場の表現として $$「場」を「電気力線」という線の束で表す$$ ことで、見えない場を視覚化できる。


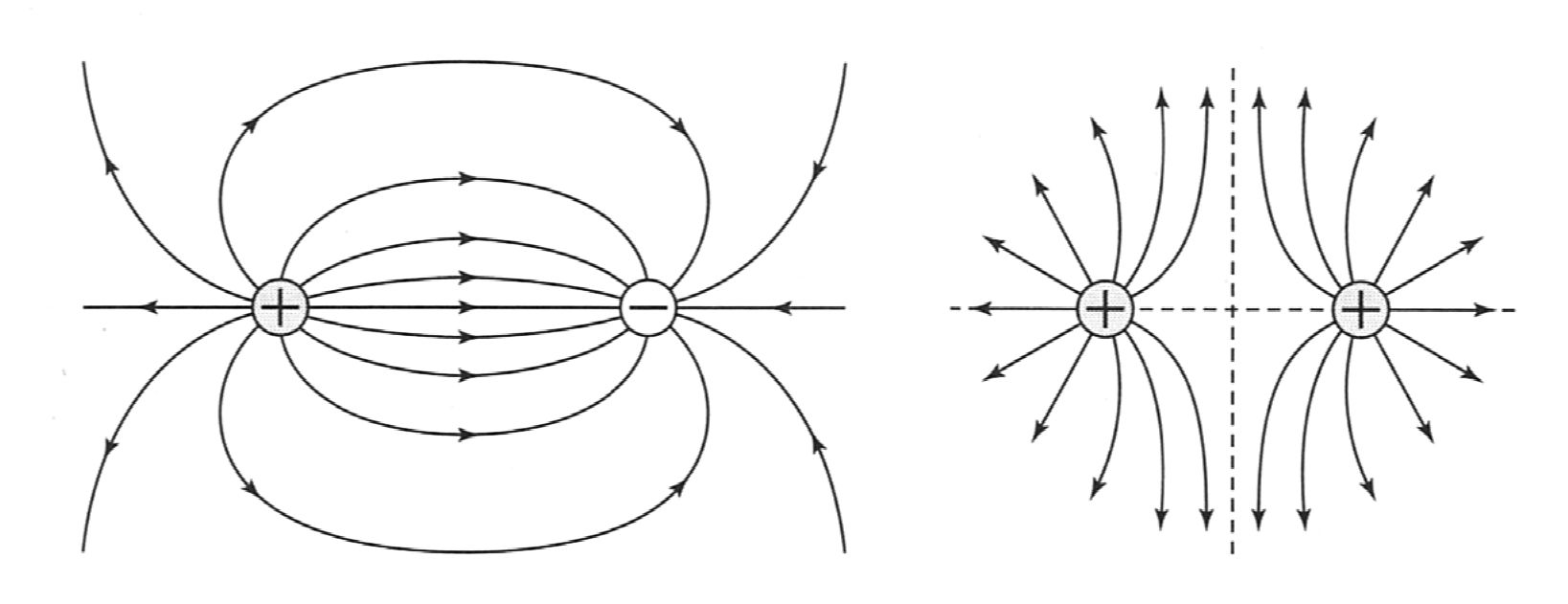
ここで、電場を「電気力線で定義」して再定義する。 と定義する。
すると、点電荷 $q$ の中心から距離 $r$ 離れた位置の電場の大きさは
(エ)より $$\therefore　電場~E=k_0\frac{q}{r^2}~~[~\mathrm{本/m^2}~]　\cdots(オ)$$ ともいえる。一方で、距離 $r$ の位置の球面の表面積 $S$ は $$S=4\pi r^2~~[~\mathrm{m^2}~]$$ なので、 点電荷$q$ から出ている電気力線総本数 $\Sigma (~E~)$ は $$\Sigma E = 4\pi r^2 \times E$$ $$=4\pi r^2 \times k_0\frac{q}{r^2}$$ つまり、 ことになる。

以上より、 ことを $$「ガウスの法則」$$ という。