今回は、「剛体のつり合い」についての話題です。
では、さっそく、考えてみましょう。
問題
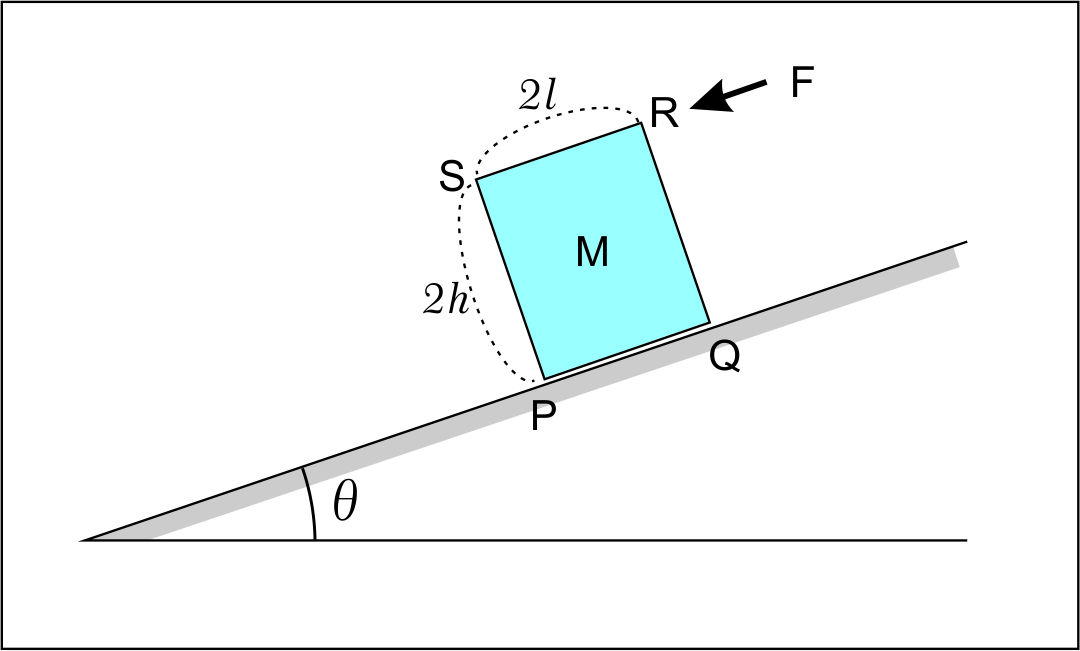
図のように、水平面と角 $\theta$ をなす粗い斜面上に、一様な質量$M$の直方体PQRSを、 長さ$\ell$ の辺を斜面の最大傾斜線に沿うように置いたら、直方体は滑ることも倒れることも なかった。斜面に垂直な方向の直方体の辺の長さは$h$ である。 直方体と斜面の間の最大静止摩擦係数を$\mu_0$ とし、重力加速度の大きさを$g$ とする。
(問い) この直方体の点Rに、斜面と平行下向きに、0から次第に大きくなる外力$F$ を加えたとき、直方体が滑る前に倒れるための $\mu_0$ に対する条件を求めよ。

図のように、水平面と角 $\theta$ をなす粗い斜面上に、一様な質量$M$の直方体PQRSを、 長さ$\ell$ の辺を斜面の最大傾斜線に沿うように置いたら、直方体は滑ることも倒れることも なかった。斜面に垂直な方向の直方体の辺の長さは$h$ である。 直方体と斜面の間の最大静止摩擦係数を$\mu_0$ とし、重力加速度の大きさを$g$ とする。
(問い) この直方体の点Rに、斜面と平行下向きに、0から次第に大きくなる外力$F$ を加えたとき、直方体が滑る前に倒れるための $\mu_0$ に対する条件を求めよ。
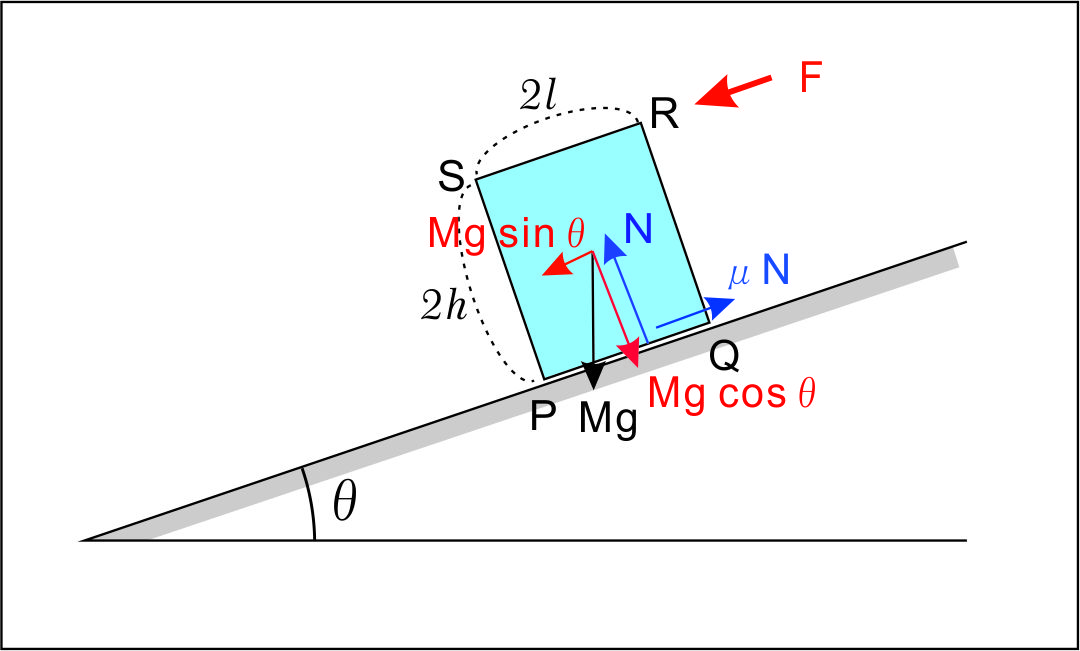
直方体にはたらく重力と外力の点P まわりのモーメントの和が反時計回りになれば、直方体は倒れるので、 倒れる条件は、
$$F\cdot 2h + Mg\sin\theta\cdot h > Mg\cos\theta\cdot \ell \cdots(ア)$$ が成立する。
(ア)より、 $$\therefore F > \frac{Mg}{2h}(\ell\cos\theta-h\sin\theta) \cdots(イ)$$ 直方体に働く垂直抗力の大きさは、斜面垂直方向の力のつり合いから、 $$N=Mg\cos\theta$$ となるから、最大摩擦力$f_{max}$は、 $$f_{max}=\mu_0 N=\mu_0 Mg\cos\theta$$ 直方体にはたらく力の斜面に沿った下向き成分は、$Mg\sin\theta + F$ であるから、 直方体が滑らない条件は $$Mg\sin\theta+F \leqq \mu_0 Mg\cos\theta$$ $$\therefore F\leqq Mg(\mu_0\cos\theta-\sin\theta) \cdots(ウ)$$ (イ)、(ウ)より、 $$\frac{Mg}{2h}(\ell\cos\theta-h\sin\theta)< F\leqq Mg(\mu_0\cos\theta-\sin\theta)$$ となる。これより、 $$\frac{Mg}{2h}(\ell\cos\theta-h\sin\theta) < Mg(\mu_0\cos\theta-\sin\theta)$$ $$\ell\cos\theta-h\sin\theta < 2h(\mu_0\cos\theta-\sin\theta)$$ $$2h\cos\theta > \ell\cos\theta+h\sin\theta$$ よって、求める条件は、 $$\therefore \mu_0 > \frac{1}{2}\left(\frac{\ell}{h}+\tan\theta\right) //$$
いかがでしたか。
理解は出来ましたか?
では、また次回にお会いしましょう。