という「ケプラーの第１法則」を前提として、「楕円軌道の極座標表示」を与えた所からスタートする。

いま、質量 $M$ の太陽のまわりを質量 $m$ の惑星が「万有引力」をうけて公転しているときを考え、 $G$ を万有引力定数とする。



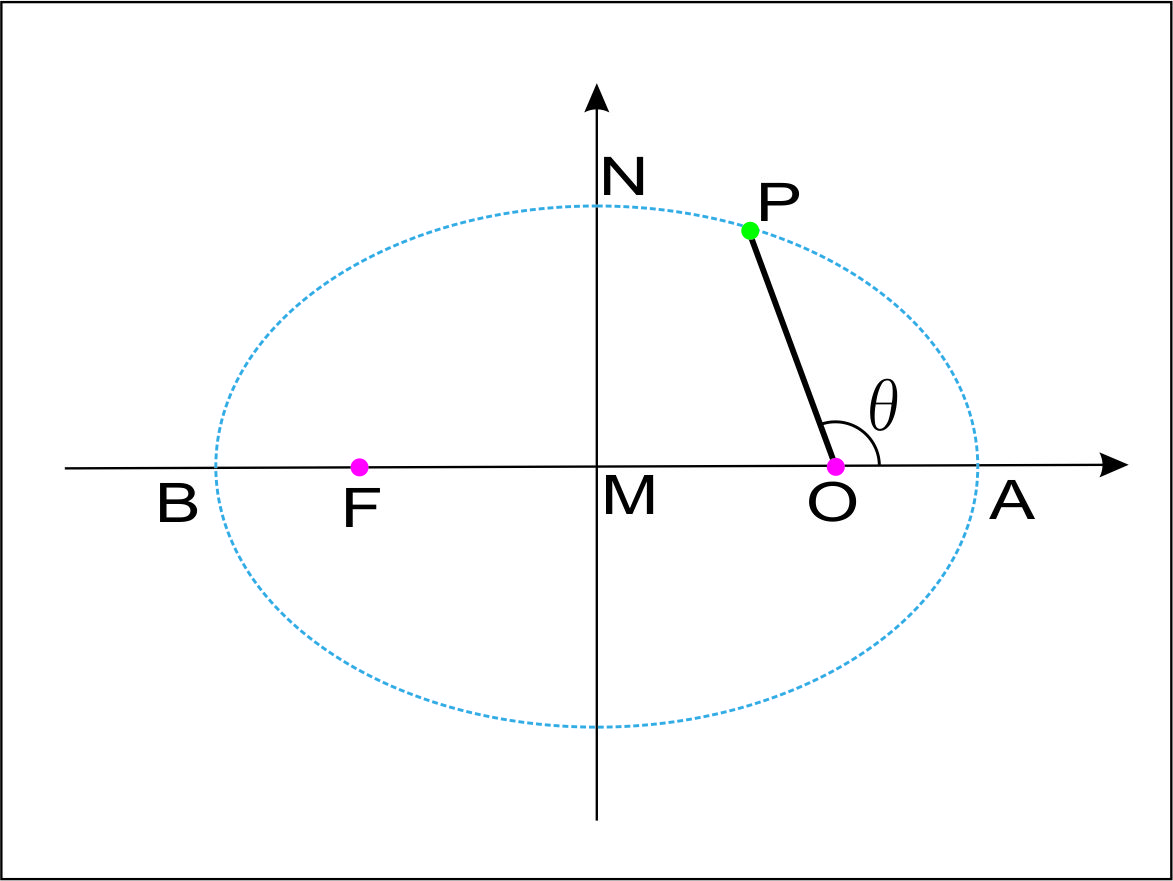
楕円を表す極座標表示は $$r=\frac{\ell}{1+e\cos\theta}~~~~(0 < e < 1)~~　\cdots(ア)$$ で与えられることを前提とする。ただし、 $$h=r^2\cdot\dfrac{d\theta}{dt}、\ell = \frac{h^2}{GM}、e = \frac{h^2C}{GM}~~(Cは定数)　\cdots(イ)$$ である。
$$\mathrm{OA}=\frac{\ell}{1+e}、\mathrm{OB}=\frac{\ell}{1-e}$$ により、 $$(長半径) = \frac{\mathrm{OA}+\mathrm{OB}}{2}$$ $$=\frac{1}{2}\cdot\left(\frac{\ell}{1+e}+\frac{\ell}{1-e}\right)$$ $$\therefore　(長半径) = \frac{\ell}{1-e^2}　\cdots(ウ)$$ また、 $$\mathrm{MO} = (長半径) - \mathrm{OA}=\frac{\ell}{1-e^2}-\frac{\ell}{1+e}$$ $$\therefore　 \mathrm{MO}=\frac{\ell e}{1-e^2}　\cdots(エ)$$ P がN にきたときには $$r\cos\theta= - \mathrm{MO}$$ になることを利用すると、楕円の式から $$\mathrm{ON} = \frac{\ell}{1-e^2}　\cdots(オ)$$ であることが分かり、 $$\mathrm{MN}^2=\mathrm{ON}^2-\mathrm{MO}^2$$ (エ)、(オ)より、 $$\mathrm{MN}^2 = \left(\frac{\ell}{1-e^2}\right)^2 - \left(\frac{\ell e}{1-e^2}\right)^2$$ $$=\frac{\ell}{1-e^2}$$ $$\therefore　(短半径) = \mathrm{MN} = \frac{\ell}{\sqrt{1-e^2}}　\cdots(カ)$$ となる。

ここで、 $$(楕円の面積) = \pi\times(長半径)\times(短半径)$$ であるから、 $$(楕円の面積) = \pi\times\frac{\ell e}{1-e^2}\times\frac{\ell}{\sqrt{1-e^2}}$$ $$\therefore　(楕円の面積) = \frac{\pi \ell^2}{(1-e^2)^{3/2}}　\cdots(キ)$$ ここで、(イ)から、 $$\therefore　(面積速度) = \frac{1}{2}r^2\frac{d\theta}{dt}= \frac{h}{2}　\cdots(ク)$$ より、(楕円の面積)を(面積速度)で割れば、 $$楕円を一周するのに要する時間、つまり「周期T」$$ が求められる。 $$T = \frac{\pi \ell^2}{(1-e^2)^{3/2}}\div \frac{h}{2}$$ $$\therefore　T = \frac{2\pi \ell^2}{h(1-e^2)^{3/2}}　\cdots(ケ)$$ これを２乗し、(イ)の $$\ell = \frac{h^2}{GM}$$ より、 $$h^2=\ell GM$$ を用いると、 $$T^2 = \frac{4\pi^2\ell^4}{h^2(1-e^2)^3}$$ $$=\frac{4\pi^2}{GM}\left(\frac{\ell}{1-e^2}\right)^3$$ (ウ)より、 $$\therefore　T^2 = \frac{4\pi^2}{GM}\times (長半径)^3 　\cdots(コ)$$ が結論として導かれる。

これは

公転周期の２乗は軌道の長半径の３乗に比例する

ことを示しているので、「ケプラーの第３法則」が導かれたことになる 。