図１に示すように、水平な床面上に質量 $m$ の物体 A を置き、軽いばねを取りつける。 ばねが床面と水平になるように、ばねの他端の壁に固定する。 物体Aは図の $x$ 軸上を運動し、その位置を座標 $x$ で表す。 ばねが自然の長さ $\ell$ のとき物体A の位置を原点 $x=0$ にとり、 ばね定数を $k$ とする。 物体A と床面との間の最大静止摩擦係数を $\mu'$ 、動摩擦係数を $\mu$ とする。 また、重力加速度の大きさを $g$ とし、ばねの質量は無視できるものとする。


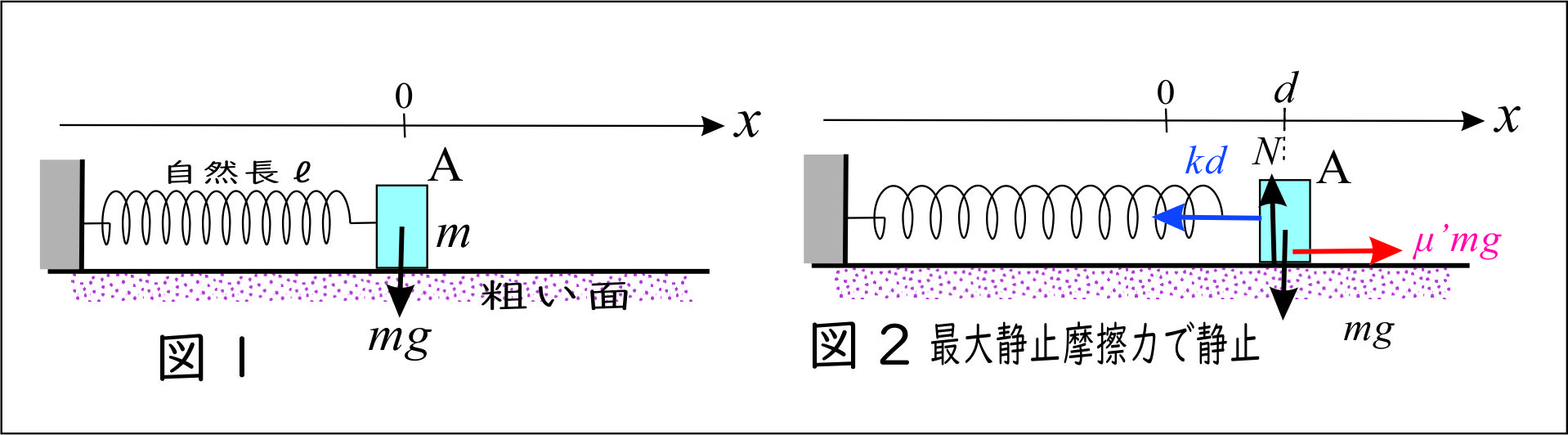
原点Oからの距離が $d$ より小さいとその位置で静止しているが、 $d$ を少しでも超えると、 物体Aは滑り出すとする。
このとき、図２より、 $$\mu'mg - kd = 0　\cdots(ア)$$ $$\therefore　d=\frac{\mu'mg}{k}　\cdots(イ)$$ が成立する。

いま、$x = x_0~( > d)$ の位置まで引き伸ばし、静かに放した(図３)。



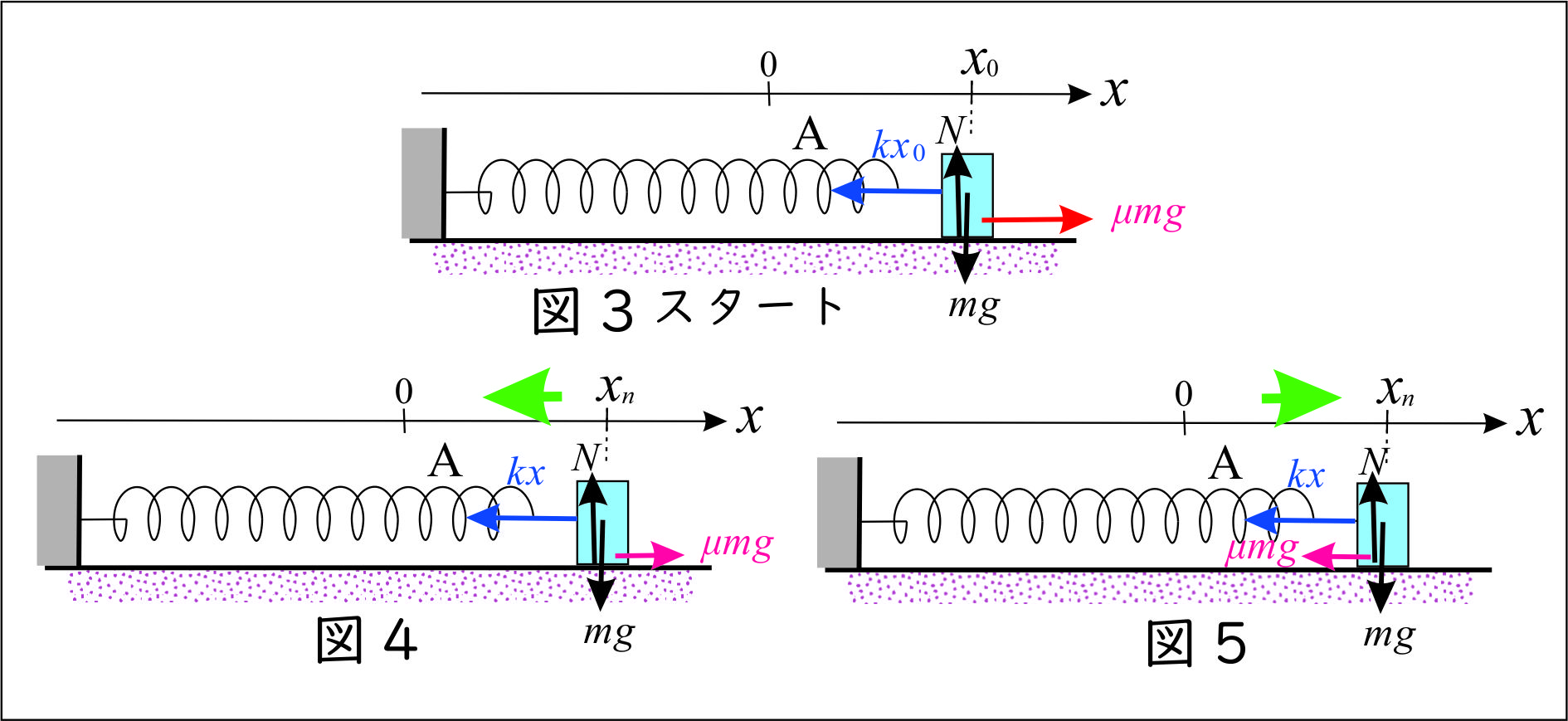
このとき、運動方程式は、

●『左に進行している』(図４)とき、 $$m\frac{d^2x}{dt^2}= -kx+\mu mg$$ $$\therefore　\frac{d^2x}{dt^2}= -\frac{k}{m}\cdot\left( x - \frac{\mu mg}{k}\right)　\cdots(ウ)$$ (ウ)において、$x-\dfrac{\mu mg}{k}= X$ とおくと、 $$\therefore　\frac{d^2x}{dt^2}= -\frac{k}{m}\cdot X　\cdots(エ)$$ となり、 $$振動の中心は x= \frac{\mu mg}{k}$$ となる。
また、折り返す前までに $$\frac{\mu mg}{k}\times 2 = \frac{2\mu mg}{k}~だけ移動距離が減少する。$$
●『右に進行している』(図５)とき、 $$m\frac{d^2x}{dt^2}= -kx-\mu mg$$ $$\therefore　\frac{d^2x}{dt^2}= -\frac{k}{m}\cdot\left( x + \frac{\mu mg}{k}\right)　\cdots(オ)$$ (オ)において、$x+\dfrac{\mu mg}{k}= X$ とおくと、 $$\therefore　\frac{d^2x}{dt^2}= -\frac{k}{m}\cdot X　\cdots(カ)$$ となり、 $$振動の中心は x= -\frac{\mu mg}{k}$$ となる。
また、折り返す前までに $$\frac{\mu mg}{k}\times 2 = \frac{2\mu mg}{k}~だけ移動距離が減少する。$$

＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊
以上より、 $$『片道につき \dfrac{2\mu mg}{k} ずつ移動距離は減少する』\cdots(キ)$$ 【 減衰振動 】の運動をし、 折り返しが $n$ 回行われた後の折り返し点 $X(n)$ は、 $$|X(n)| =|x_0| - \frac{2\mu mg}{k}\times n　\cdots(ク)$$
そして、 $$|X(n)| \leqq d　となると、静止する。$$



＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊

また、(エ)、(カ)より、角振動数を $\omega$ とすると、 $$\omega = \sqrt{\frac{k}{m}}$$ であり、 $$\therefore　周期T = \frac{2\pi}{\omega}=2\pi\sqrt{\frac{m}{k}}　\cdots(ケ)$$ となる。
これは、Aが左に進む場合と右に進む場合とで、 振動の中心は異なるが、 $$減衰振動でも、周期に影響はない$$ という事を示している。

ここで、エネルギーについて考えよう。

(ウ)、(オ)より、 $$\frac{d^2x}{dt^2} = -\frac{k}{m}x \mp\mu g$$ $$\frac{dx}{dt}\cdot \frac{d}{dt}= -\frac{k}{m}\cdot x \mp\mu g$$ $$\frac{dx}{dt}\cdot \frac{d}{dt}\cdot dx= -\frac{k}{m}\cdot x\cdot dx \mp\mu g\cdot dx$$ $$\int\frac{dx}{dt}\cdot \frac{d}{dt}\left(\frac{dx}{dt}\right)\cdot dt= -\frac{k}{m}\int x\ dx \mp\mu g\int dx$$ ここで、 $$\frac{dx}{dt}=v$$ とおくと、 $$\frac{1}{2}v^2 = -\frac{k}{m}\cdot\frac{1}{2}x^2\mp\mu g x + C$$ $$\frac{1}{2}mv^2 = -\frac{1}{2}kx^2\mp\mu mg x + C_1$$ よって、 $$\therefore　\frac{1}{2}mv^2 + \frac{1}{2}kx^2\pm\mu mg x ~=~ 一定　\cdots(コ)$$ が導かれる。

これは、 $$力学的エネルギー保存の法則は成り立たない$$ が、 $$『外力のした仕事』を含めると、エネルギー保存が成立する。$$ という事を示している。

言い換えれば、 $$外力がした仕事の分だけ力学的エネルギーは増減する$$ ということである。