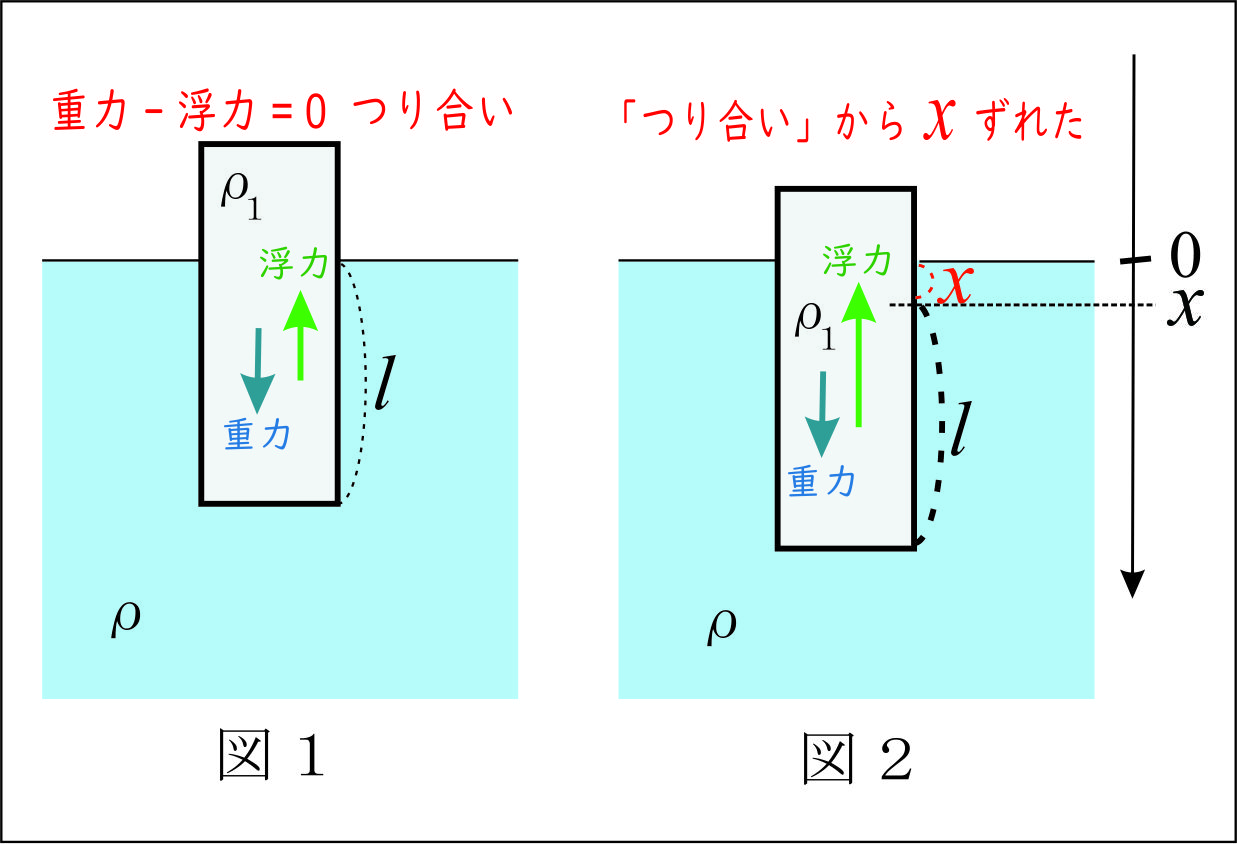
表面積$S$、高さ$L$の円柱状の木片Aを水に浮かべると、長さ $\ell$ だけ沈んだ（図１）。 木片は水中を抵抗がなくなめらかに運動し、水面のゆれや表面張力は無視する。 また、すべての運動は鉛直方向のみを考え、横ゆれや回転運動などはしないものとする。 水の密度を$\rho$ 、木片Aの密度を $\rho_1$ 、重力加速度を $g$ とする。

木片Aの質量は、$\rho_1LS$ であり、木片Aが排除した水の質量が$\rho \ell S$ なので、 図１の「つり合いの位置にある」とき、 $$\rho_1LS - \rho \ell S =0　\cdots(ア)$$ が成立する。

ここで、つり合いの位置から木片Aを $x$ だけ移動させる（図２）と、運動方程式は、 $$\rho_1LS\cdot \frac{d^2x}{dt^2}=\rho_1LS \cdot g - \rho S g(l + x)　\cdots(イ)$$ (ア)より、(イ)は、 $$\rho_1LS\cdot \frac{d^2x}{dt^2} = - \rho S g \cdot x$$ $$\therefore　 \frac{d^2x}{dt^2} = - \frac{\rho g}{\rho_1 L}\cdot x　\cdots(ウ)$$ ここで、単振動の角振動数を $\omega$ とすると、 $$\frac{d^2x}{dt^2}=-\omega^2x　\cdots(エ)$$ と表されるので、
(ウ)、(エ)を比較して、 $$\omega^2 = \frac{\rho g}{\rho_1 L}$$ $$\therefore　\omega = \sqrt{ \frac{\rho g}{\rho_1 L}}　\cdots(オ)$$ となる。

よって、木片Aは、角振動数 $\omega = \sqrt{ \dfrac{\rho g}{\rho_1 L}}$ の単振動をし、 $$\therefore　周期T=\frac{2\pi}{\omega}=2\pi\sqrt{\frac{\rho_1L}{\rho g}}　\cdots(カ)$$ である。