今日も晴天が続いていますが、空気がとても冷たいです。
さて、今回は「反射問題」です。この手の問題では、
ポイント
反射問題では、図形を折り返して、経路を直線にして考える。
ということがポイントになります。
では、さっそく、考えてみましょう。
問題
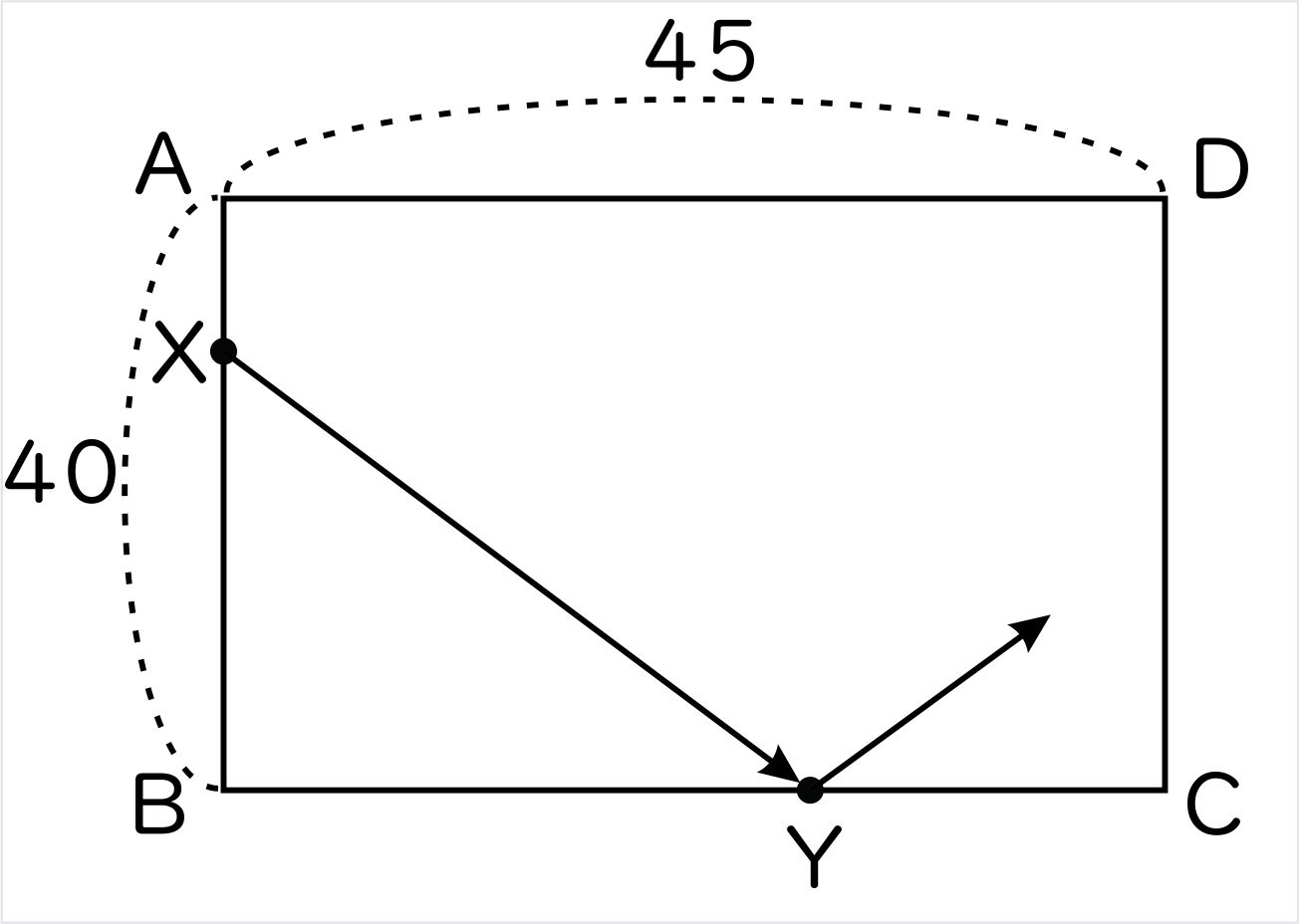
AB = 40 (cm)、AD = 45 (cm) の長方形ABCDがあります。 辺AB上にある点Xから辺BC上にある点Yに向けて点Pが発射され、次のルールに従って 点Pはまっすぐ進むものとする。
< ルール >
- 点Pは各辺にあたると図 1 のようにはねかえる。
- 点Pは頂点A, B, C, D のいずれかにあたると止まる。
- 点Pは発射されてから止まるまで一定の速さ $v$ (cm 毎秒)で進む。
[ 問い ] AX = 5 (cm)$,$ BY = 30 (cm)で、点Pが点Xから点Yに到達するのに3秒かかるとき、点Pが発射されてから点Pはどの頂点に何秒後に止まりますか。
36と45の最小公倍数は、180なので、

図より、点Pは、点B で止まる。
このとき、
点Pが横方向に1 cm 進むのに$\dfrac{2}{36}$秒かかるから、 点Pが出発点Aから終点Bで止まるまでに、横方向に$45\times4=180$ cm 進む。 $$\frac{2}{36}\times 180 = 10 秒かかる。$$ したがって、 $$\therefore 点Pは10秒後に点Bで止まる。$$

図より、点Pは、点B で止まる。
このとき、
点Pが横方向に1 cm 進むのに$\dfrac{2}{36}$秒かかるから、 点Pが出発点Aから終点Bで止まるまでに、横方向に$45\times4=180$ cm 進む。 $$\frac{2}{36}\times 180 = 10 秒かかる。$$ したがって、 $$\therefore 点Pは10秒後に点Bで止まる。$$
いかがでしたか。
理解は出来ましたか?
では、また次回にお会いしましょう。