今回は、「格子点問題」の話題です。
これも定番問題なので、未経験の人はここで理解してしまおう。
では、始めよう。
ポイント
縦、横それぞれで、辺を横切った数に注目して考える。
ということがポイントになります。
では、さっそく、考えてみましょう。
問題
いくつかの正方形のマスをすきまなく並べて作った長方形の左上の頂点をA、左下の頂点をB、右下の頂点をC、
右上の頂点をDとします。
いま、$2000\times2022$ (縦に2000個、横に2022個)のマスで作られた長方形ABCDを考える。この長方形に対角線ACと対角線BDを引いたとき、対角線が一本も通らないマスはいくつあるか。
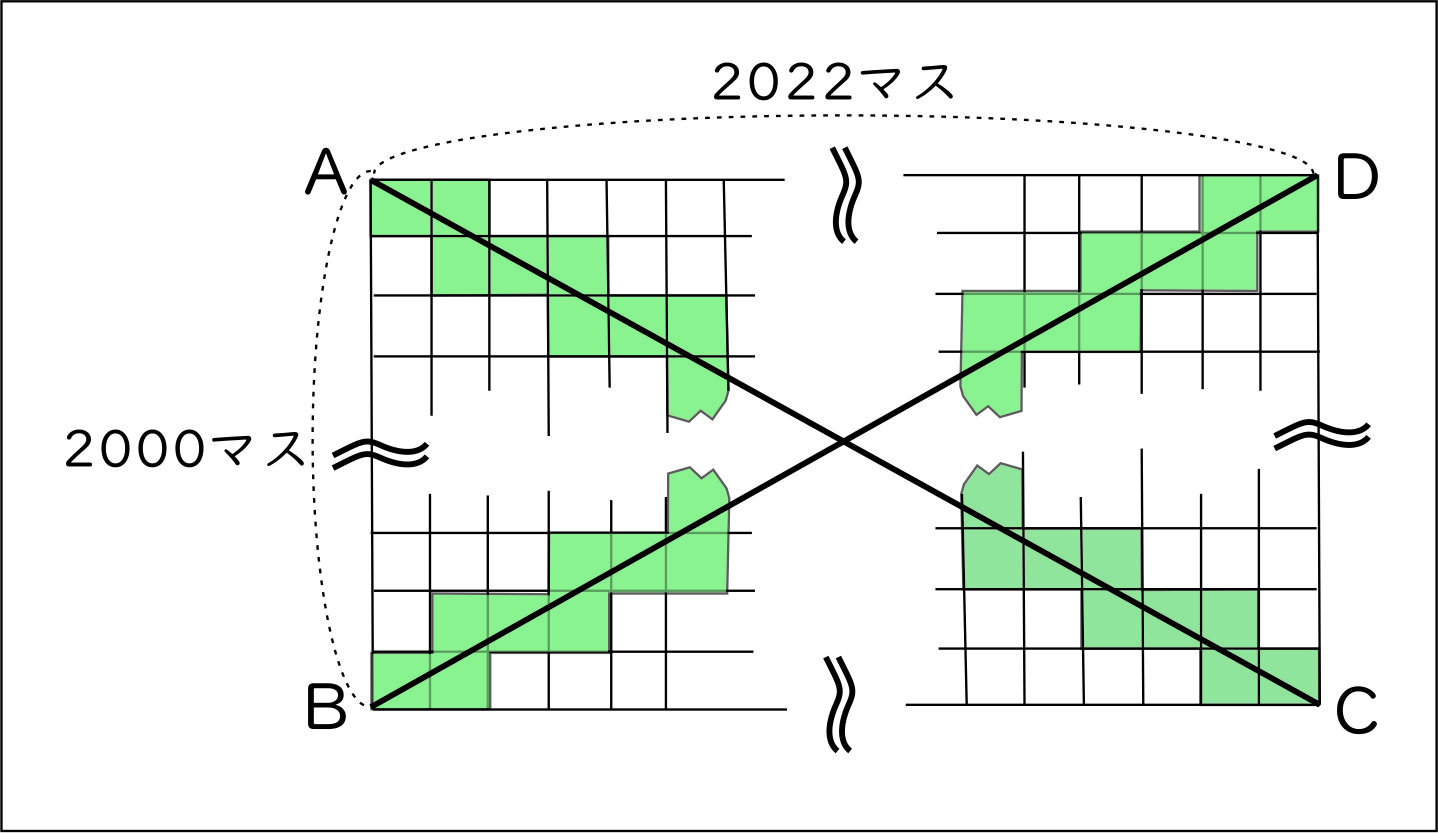
いま、$2000\times2022$ (縦に2000個、横に2022個)のマスで作られた長方形ABCDを考える。この長方形に対角線ACと対角線BDを引いたとき、対角線が一本も通らないマスはいくつあるか。

対角線AC、BDそれぞれにおいて、対角線がもとのマスの縦の線や横の線と交わるごとに、
マスを1個通ることになります。
2000と2022の最大公約数は2なので、$1000\times1011$のマスで作られた長方形が 横に2個、縦に2個並ぶ。
この$1000\times1011$のマスで作られた長方形Sの対角線の1本は、縦の線とは1011回、横の線とは1000回交わります。最後の交わりは長方形の頂点で、 縦と横の両方で数えているので、対角線が通るマスは、 $$1011+1000-1 = 2010 (個)。$$ ここで、対角線AC上には、長方形Sが、すきまなく重なりもなく、ちょうど2個並ぶ。
よって、対角線ACが通るマスは、 $$\therefore 2010\times2 = 4020 個。$$ また、対角線BDについても同様にして4020個ですが、対角線ACとBDの両方を通るマスがるかどうかを 考えると、縦ABと横ADともに偶数なので、対角線AC、BDの交点はマス目の頂点にあるので、 両方通るマスはありません。つまり、0個。 よって、対角線ACとBDの少なくとも一方が通るマスは、 $$\therefore 4020 + 4020 - 0 = 8040 個。$$ したがって、対角線が一本も通らないマスの個数は $$\therefore 2000\times2022 - 8040 = 4035960 個$$
2000と2022の最大公約数は2なので、$1000\times1011$のマスで作られた長方形が 横に2個、縦に2個並ぶ。
この$1000\times1011$のマスで作られた長方形Sの対角線の1本は、縦の線とは1011回、横の線とは1000回交わります。最後の交わりは長方形の頂点で、 縦と横の両方で数えているので、対角線が通るマスは、 $$1011+1000-1 = 2010 (個)。$$ ここで、対角線AC上には、長方形Sが、すきまなく重なりもなく、ちょうど2個並ぶ。
よって、対角線ACが通るマスは、 $$\therefore 2010\times2 = 4020 個。$$ また、対角線BDについても同様にして4020個ですが、対角線ACとBDの両方を通るマスがるかどうかを 考えると、縦ABと横ADともに偶数なので、対角線AC、BDの交点はマス目の頂点にあるので、 両方通るマスはありません。つまり、0個。 よって、対角線ACとBDの少なくとも一方が通るマスは、 $$\therefore 4020 + 4020 - 0 = 8040 個。$$ したがって、対角線が一本も通らないマスの個数は $$\therefore 2000\times2022 - 8040 = 4035960 個$$
いかがでしたか。
理解は出来ましたか?
では、また次回にお会いしましょう。