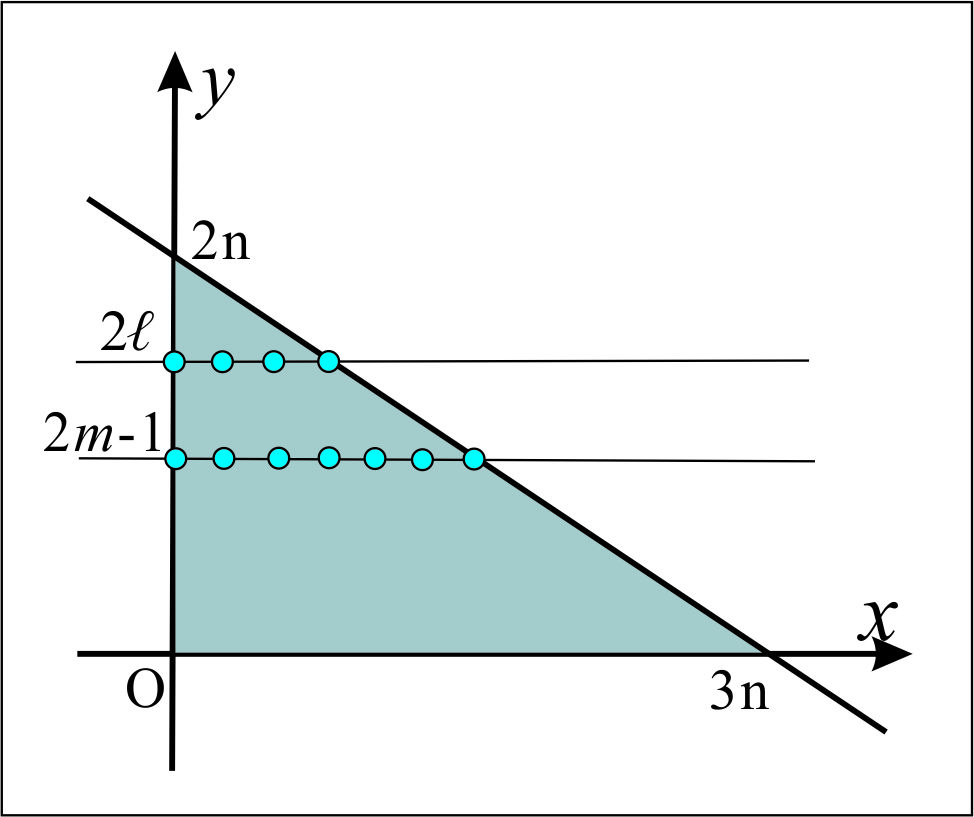
題意の領域 $D$ は $$x\geqq0　\cdots(ア)$$ $$y\geqq0　\cdots(イ)$$ $$2x+3y\leqq6n　\cdots(ウ)$$ で表される。
ここで、$y=t ~~(0\leqq t \leqq 2n)$ における切り口を考えるとき、 $t$ が偶奇によって状態が変わるので、

• 　$t=2\ell$ のとき、領域$D$内の$y=2\ell$ 上の格子点の個数を考える。
  (ウ)より、 $$2x+3\cdot 2\ell \leqq 6n$$ であるから、(ア)とあわせて、 $$\therefore 0\leqq x \leqq 3n - 3\ell　\cdots(エ)$$ ここで、$0 \leqq 2\ell \leqq 2n$ より、$0\leqq \ell \leqq n$ の範囲に整数 $x$ は、 $$\therefore　3n-3\ell +1~~個　\cdots(オ)$$ ある。
• 　$t=2m-1$ のとき、領域$D$内の$y=2m-1$ 上の格子点の個数を考える。
  (ウ)より、 $$2x+3\cdot (2m-1) \leqq 6n$$ であるから、(ア)とあわせて、 $$\therefore 0\leqq x \leqq 3n - 3m +\frac{3}{2}　\cdots(カ)$$ ここで、$0 \leqq 2m-1 \leqq 2n$ より、$1\leqq m \leqq n$ の範囲に整数 $x$ は、 $$\therefore　3n-3m +2~~個　\cdots(キ)$$ ある。
  よって、以上 i), ii) より、求める格子点の個数は、 $$\sum_{\ell=0}^{n}(3n-3\ell +1)+\sum_{m=1}^n(3n-3m+2)$$ $$=\sum_{\ell=0}^{n}\{(3n+1)-3\ell\}+\sum_{m=1}^n\{(3n+2)-3m\}$$ $$=(3n+1)(n+1)-3\cdot\frac{n(n+1)}{2}$$ $$+(3n+2)n-3\cdot\frac{n(n+1)}{2}$$ $$=3n^2+4n+1-(3n^2+3n)+3n^2+2n$$ $$=3n^2+3n+1　個。　//$$