今回は、「溶解度」についての話題です。。。
ポイント
- 水和水を持つ物質(水和物)の溶解度は、水100 g に溶ける無水物の質量で表す。
- 【ヘンリーの法則】 溶解度が比較的小さい気体では、一定温度で、一定量の溶媒に溶ける物質量(質量) は、気体の圧力(分圧)に比例する。また、一定量の溶媒に溶ける気体の体積は、(その圧力下で測定すれば )圧力に無関係に一定である。
ということがポイントになります。
では、さっそく、考えてみましょう。
問題
次の各問いに答えなさい。
次の各問いに答えなさい。
- 35℃で水50.0gに CuSO$_4\cdot$H$_2$O の結晶は 25.8 g まで溶ける。 このことから、 35℃で水100gに対するCuSO$_4$ の溶解度を求めよ。 ただし、 式量は CuSO$_4$ = 160、H$_2$O = 18.0 とする。
- 80℃の CuSO$_4$ の飽和水溶液100g を35℃ まで冷却すると、CuSO$_4\cdot$5H$_2$O の 結晶が何g析出するか。ただし、80℃における CuSO$_4$ の溶解度は56.0である。
- CuSO$_4\cdot$5H$_2$O 25.8 g 中の無水物と水和水の質量は $$\mathrm{CuSO}_4\cdot5\mathrm{H}_2\mathrm{O}=160+18\times5=250$$ $$\mathrm{CuSO}_4 = 160$$ より、 $$無水物:~25.8\times\frac{160}{250}=16.512 \approx 16.5~[~\mathrm{g}~]$$ $$水和水:~25.8-16.5=9.3~[~\mathrm{g}~]$$ よって、求める溶解度を$S$とすると $$\frac{溶質量}{溶媒量}=\frac{16.5}{50.0+9.3}=\frac{S}{100}$$ $$\therefore S=27.824\cdots\approx 27.8~[~\mathrm{g}~] //$$
- 80℃の飽和溶液100g中に含まれる CuSO$_4$(無水物)の質量は
$$100\times\frac{56.0}{100+56.0}=35.897\cdots\approx 35.9~[~\mathrm{g}~]$$
水の質量は
$$100-35.9=64.1~[~\mathrm{g}~]$$
ここで、 CuSO$_4\cdot$5H$_2$O の結晶が $x$ [ g ] 析出したとすると、
$$\mathrm{CuSO}_4~:~\frac{160}{250}x~[~\mathrm{g}~]$$
$$5\mathrm{H}_2\mathrm{O}~:~\frac{90}{250}x~[~\mathrm{g}~]$$
である。
結晶析出後の残溶液は35℃の飽和溶液であることから、 $$\frac{溶質量}{溶液量}=\frac{35.9-\dfrac{160}{250}x}{100-x}=\frac{27.8}{100+27.8}$$ $$\therefore x=33.486\cdots\approx 33.5~[~\mathrm{g}~] //$$
問題
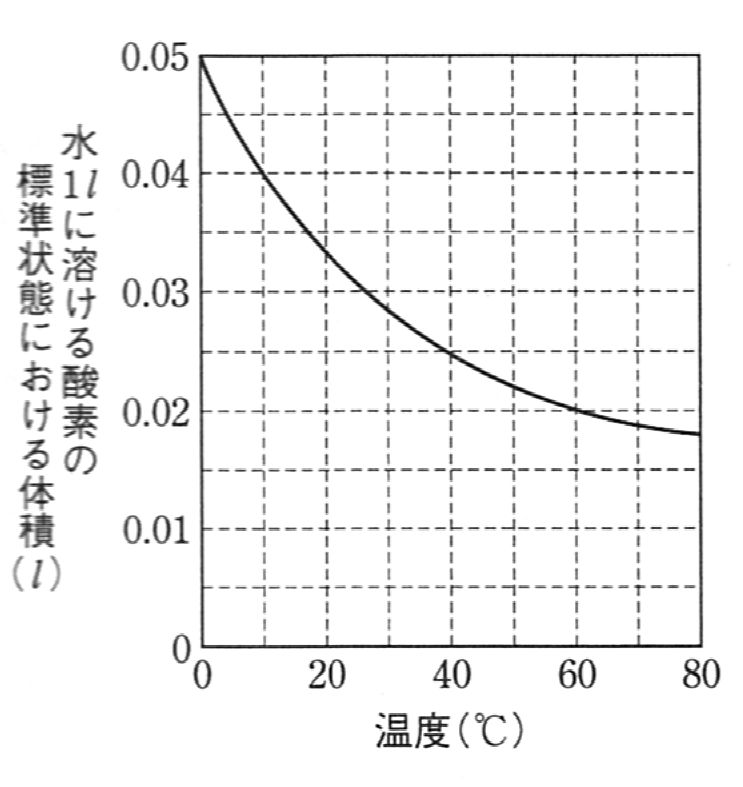
気体の溶解度は、1気圧の気体が溶媒1 $\ell$ に溶けるときの気体の体積 [ $\ell$ ] を 標準状態 に換算した数値で表される。図に0℃から80℃での水に対する酸素の溶解度曲線を示す。 この溶解度曲線を用いると、1気圧の空気と接している水2.0 $\ell$ の温度を10℃から60℃に上げたとき、 溶けきれずに出てくる気体に含まれる酸素の質量は何g か。ただし、空気は窒素 : 酸素 = 4 : 1 (体積比) の混合気体とし、原子量はO = 16 とする。

気体の溶解度は、1気圧の気体が溶媒1 $\ell$ に溶けるときの気体の体積 [ $\ell$ ] を 標準状態 に換算した数値で表される。図に0℃から80℃での水に対する酸素の溶解度曲線を示す。 この溶解度曲線を用いると、1気圧の空気と接している水2.0 $\ell$ の温度を10℃から60℃に上げたとき、 溶けきれずに出てくる気体に含まれる酸素の質量は何g か。ただし、空気は窒素 : 酸素 = 4 : 1 (体積比) の混合気体とし、原子量はO = 16 とする。
グラフより、酸素は10℃で水1.0$ \ell$ に対して0.04 $\ell$ 溶ける。
これは標準状態に換算した体積なので、物質量は$\dfrac{0.04}{22.4}$ mol 。
また、酸素の分圧は、全圧(1気圧=$1.0\times10^5$Pa) の$\dfrac{1}{5}$ で、$2.0\times10^4$ Pa である。
よって、水2.0 $\ell$ に溶けている酸素は $$分圧に比例し、溶かす水の体積にも比例する$$ から、 $$\frac{0.04}{22.4}\times\frac{2.0\times10^4}{1.0\times10^5}\times\frac{2.0}{1.0}~~[~\mathrm{mol}~]$$ 同様に、60℃では、 $$\frac{0.02}{22.4}\times\frac{2.0\times10^4}{1.0\times10^5}\times\frac{2.0}{1.0}~~[~\mathrm{mol}~]$$ したがって、出てくる酸素(O$_2$=32) は、 $$\frac{0.04-0.02}{22.4}\times\frac{2.0\times10^4}{1.0\times10^5}\times\frac{2.0}{1.0}~~[~\mathrm{mol}~]$$ $$= 0.01142\cdots \approx 0.011~[~\mathrm{g}~] //$$
よって、水2.0 $\ell$ に溶けている酸素は $$分圧に比例し、溶かす水の体積にも比例する$$ から、 $$\frac{0.04}{22.4}\times\frac{2.0\times10^4}{1.0\times10^5}\times\frac{2.0}{1.0}~~[~\mathrm{mol}~]$$ 同様に、60℃では、 $$\frac{0.02}{22.4}\times\frac{2.0\times10^4}{1.0\times10^5}\times\frac{2.0}{1.0}~~[~\mathrm{mol}~]$$ したがって、出てくる酸素(O$_2$=32) は、 $$\frac{0.04-0.02}{22.4}\times\frac{2.0\times10^4}{1.0\times10^5}\times\frac{2.0}{1.0}~~[~\mathrm{mol}~]$$ $$= 0.01142\cdots \approx 0.011~[~\mathrm{g}~] //$$
いかがでしたか。
理解は出来ましたか?
では、また次回にお会いしましょう。