数学フォローアップ【旧コンテンツ】

ポイント

問題

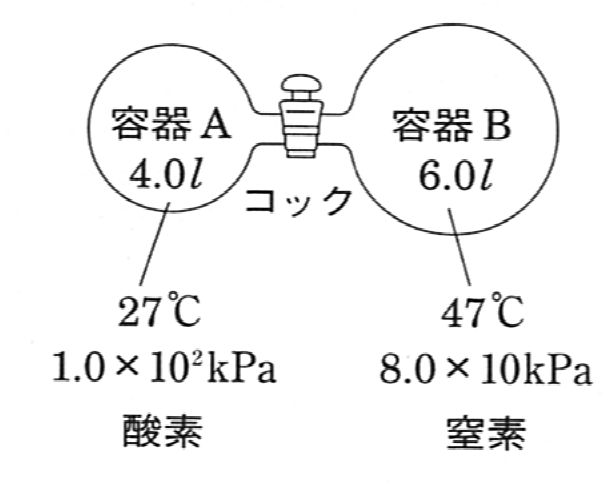
図のようなコックで連結された容器A (4.0 $\ell$) と容器B (6.0 $\ell$) がある。容器 A には 27℃、$1.0\times10^2 $kPa の酸素を、容器B には 47℃、$8.0\times10$kPa の窒素を詰めた。次の各問いに答えよ。

　コックを開くと、O$_2$ は容器全体に広がる(拡散)から、その体積は、 $$4.0 + 6.0 = 10.0~~(~\ell~)$$ になる。
混合後の O$_2$ の分圧を $p_{O_{2}}$ とおくと、「ボイル・シャルルの法則」より、 $$\frac{1.0\times10^2\times 4.0}{300} = \frac{p_{O_2} \times 10.0}{360}$$ $$\therefore　p_{O_2} = 4.8\times10~~[~\mathrm{kPa}~]$$ 同様に、混合後のN$_2$の分圧を $p_{N_2}$ とおくと、 $$\frac{8.0\times10\times6.0}{320} = \frac{p_{N_2}\times 10.0}{360}$$ $$\therefore　p_{N_2}=5.4\times10~[~\mathrm{kPa}~]$$ よって、 $$全圧 = p_{O_2}+p_{N_2}=(4.8\times10)+(5.4\times10)$$ $$\therefore　全圧 = 10.2\times 10 \approx 1.0\times10^2~[~\mathrm{kPa}~]　//$$
　平均分子量とは、混合気体がただ1種類の気体だけからなるとみなして求められた見かけの分子量のことである。
混合気体では、体積一定では、 $$分圧の比 ~=~ 物質量の比$$ が成り立つので、物質量の比は、 $$\mathrm{O}_2 : \mathrm{N}_2 = 4.8\times 10 : 5.4\times 10=8 : 9$$ ここで、分子量は、O$_2$=32、N$_2$=28 なので、混合気体1molの質量は、 $$32[\mathrm{g/mol}]\times\frac{8}{8+9}+28[\mathrm{g/mol}]\times\frac{9}{8+9}$$ $$= 29.882\cdots \approx 30~[~\mathrm{g/mol}~] 　//$$

問題

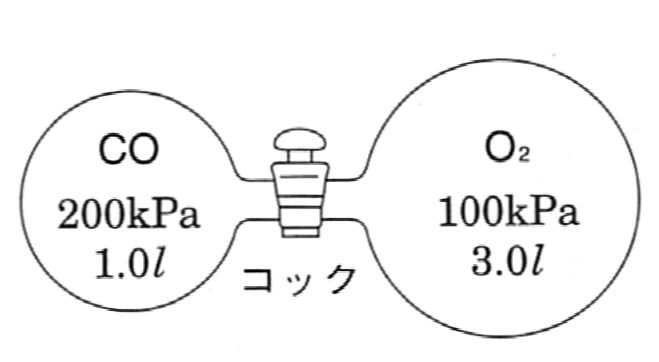
図の装置に一酸化炭素と酸素を別々に封入し、温度を 27 ℃に保った。

　CO、O$_2$ の分圧をそれぞれ $p_{CO}$、$p_{O_2}$ とすると、 $$200\times1.0=p_{CO}\times4.0$$ $$\therefore　p_{CO} = 50~[~\mathrm{kPa}~]　//$$ $$100\times3.0=p_{O_2}\times4.0$$ $$\therefore　p_{O_2} = 75~[~\mathrm{kPa}~]　//$$
　温度、体積が一定なので、 $$分圧比 ~=~ 物質量の比$$ が成り立つ。

$~~~~~~~~~~~~~~~~~~~~~~2\mathrm{CO}~~~~~ +~~~~~ \mathrm{O}_2~~~~~ \longrightarrow 2 \mathrm{CO}_2$

$反応前：~~~~50~\mathrm{kPa}~~~~~~~~~~ 75~\mathrm{kPa}~~~~~~~~~~~~ 0$

$反応後：~~~~0~\mathrm{kPa}~~~~~~~~~~ 50~\mathrm{kPa}~~~~~~~~~~ 50~\mathrm{kPa}$

以上より、 $$\therefore　全圧~=~50+50=100~[~\mathrm{kPa}~]　//$$